Автоматизированное прогнозирование параметров риска с помощью схем функциональной целостности

Общий логико-вероятностный метод является дальнейшим развитием традиционных теоретико-вероятностных методов исследования сложных систем и одновременно служит теоретической основой технологии их автоматизированного структурно-логического моделирования (АСЛМ) [7]. В отличие от ранее применяемых, данный метод использует универсальное графическое средство представления свойств подобных объектов – схемы функциональной целостности (СФЦ). При этом базирующаяся на них компьютерная технология позволяет облегчить их ввод в соответствующий программный комплекс и автоматизировать как построение эквивалентной СФЦ математической модели, так и расчет показателей безопасности, живучести и надежности функционирования исследуемых здесь сложных систем.

В методологическом плане технология АСЛМ аналогична применяемым в зарубежных программных комплексах типа Risk Spectrum или Relex, однако в ней используется три типа логических операций: И (конъюнкция), ИЛИ (дизъюнкция) и НЕ (отрицание). Применение такого (функционально полного) их блока обеспечило возможность оперирования не только монотонными моделями устойчивого функционирования систем, но также принципиально новым классом немонотонных моделей их надежности, безопасности и живучести. При этом немонотонными считаются системы, которые способны изменять выходные параметры в направлении, противоположном варьированию входных.

Как и другие методы системного анализа сложных объектов, практическое использование рассматриваемого здесь подхода и основанной на нем технологии в интересах прогнозирования параметров надежности, безопасности и живучести обычно включает четыре основных крупных этапа, которые выполняются в следующей последовательности.

1. Формализованная постановка решаемой задачи, или первичное структурно-логическое моделирование, предполагающее разработку и ввод в программный комплекс "АРБИТР" [11] не только структурной модели исследуемой системы в форме СФЦ, но также одного или нескольких логических критериев функционирования, определяющих условия реализации ею какой-либо заранее заданной задачи с определенным уровнем эффективности.

2. Построение логической модели устойчивого функционирования системы в форме минимальной дизъюнктивной нормальной булевой функции состояния всех ее элементов, однозначно определяемой СФЦ и упомянутым выше критерием. Данный этап осуществляется автоматически как для монотонных, так и для немонотонных логических функций; причем вторые могут представлять различные неприводимые комбинации первых.

3. Построение расчетного вероятностного многочлена, также выполняемое автоматически, с получением расчетного многочлена вероятностной функции при допущениях о независимости в совокупности вероятностных параметров элементов исследуемой системы, несмотря на наличие в ней зависимых событий, выделяемых и представляемых с помощью аналитического аппарата так называемых групп несовместных событий [7].

4. Вычисление вероятностных показателей исследуемых функциональных свойств системы, реализуемое автоматически и с целью априорной оценки выбранных ранее единичных количественных показателей надежности, безопасности и живучести, в том числе и после внедрения мероприятий, предлагаемых для улучшения их значений.

Сервисные средства программного комплекса с технологией АСЛМ полностью обеспечивают первый этап приведенной выше процедуры, что достигается диалоговой поддержкой ввода не только самой СФЦ и всех параметров диаграммы этого типа, но также режимов и критериев автоматизированного моделирования и расчета требуемых системных характеристик моделируемой системы. Все остальные этапы, включая построение математических моделей большой размерности и выполнение довольно сложных и трудоемких расчетов, осуществляются автоматически.

Процедура применения СФЦ подобна известным методикам построения и анализа рассмотренных ранее диаграмм влияния (графов, деревьев, сетей). Однако ей присущ ряд особенностей, которые следует учитывать при построении данных смысловых моделей и их преобразовании в знаковые (математические). Основные из них заключаются в следующем.

1. Помимо известной по табл. 9.2 символики СФЦ оперируют также графическими фигурами, сведения о которых приведены на рис. 9.6.

Построение СФЦ начинается с выявления тех элементов (i = 1, 2, ..., H) случайных бинарных ("да", "нет") событий х и логических условий 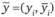их реализации или нереализации, которые считаются существенными для моделируемого процесса. Пример подобного (логически-событийного) подхода к формализованному представлению всех существенных факторов-предпосылок, необходимых и достаточных для реализации/нереализации конкретного свойства или результата отдельным элементом-узлом i, изображен на рис. 9.7 в виде фрагмента СФЦ и соответствующих ему базовых логических уравнений для прямого и инверсного выходов. Поясним, что имеющиеся там символы "&" означают конъюнкцию, т.е. используются наряду со следующим обозначением аналогичного логического оператора: "˄".

Рис. 9.6. Графические и математические символы аппарата СФЦ

Поясним, что приведенные на рис. 9.7 уравнения для у. определяют логические условия реализации соответствующей выходной функции, а для 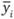– ее нереализации.

3. Подобным образом (с помощью функциональных вершин z, дизъюнктивных и конъюнктивных дуг, переменных х_i и вероятностей р.) затем представляются остальные элементы исследуемой системы, а последующее объединение полученных при этом фрагментов СФЦ позволяет логически строго и точно формализовать ее поведение в целом.

– функциональная вершина

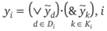– фиктивная вершина

– функциональная вершина

– фиктивная вершина

Рис. 9.7. Обобщенный фрагмент СФЦ и базовые логические уравнения

4. Применение при этом для всех функциональных и фиктивных вершин дизъюнктивных и конъюнктивных входящих дуг позволяет представлять логические условия реализации ими прямой выходной функции, а двух видов исходящих дуг – монотонные и немонотонные логические условия реализации (прямой выходу.) и нереализации (инверсный выход у.) соответствующих выходных функций как отдельными элементами, так и исследуемым объектом в целом.

5. В последующем (после ввода в программный комплекс) все эти логические переменные и вероятностные характеристики используются при автоматическом построении логических и вероятностных математических моделей исследуемой системы, необходимых для проведения их количественного анализа с целью прогнозирования ее искомых характеристик.

Для демонстрации возможности прогнозирования параметров надежности, безопасности и живучести рассмотренным выше (четырехэтапным) способом проиллюстрируем, как это делается на примере простейшей двухэлементной дублированной системы, функциональная схема (блок-схема) работоспособности которой приведена на рис. 9.8.

Рис. 9.8. Функциональная схема работоспособности системы

I. Прогнозирование показателей надежности (безотказности) системы. При построении соответствующей СФЦ (рис. 9.9) использован событийно-логический подход к анализу приведенной выше функциональной схемы и введены два случайных события и х₂, соответствующие безотказному срабатыванию элементов, представленных двумя функциональными вершинами с номерами 1 и 2 соответственно. При этом параметры надежности (безотказности, готовности) этих элементов составляют р₁ = 0,85 и р₂ = 0,95.

Показанная СФЦ является ориентированным графом, а имеющиеся в нем исходящие дуги у₁, у₂ из функциональных вершин 1 и 2 представляют логические условия реализации каждым элементом своих функций. Эти же ребра графа одновременно служат дизъюнктивными (операция ИЛИ) входящими дугами фиктивной вершины 6, которая выражает условие у₆ = y_i v y₂, являющееся логическим критерием Y_н = у₆ надежности (безотказности, готовности) рассматриваемой системы в целом.

Рис. 9.9. Схема функциональной целостности для надежности системы

В правой части рис. 9.9 приведены логические выражения для реализации выходов всех его трех вершин, которые составлены на основе базовых логических соотношений, приведенных на рис. 9.7. Эта система уравнений является точным аналитическим (логическим) аналогом разработанной СФЦ надежности системы. В программном комплексе АСЛМ такие системы формируются автоматически и используются для проведения требуемых вычислений.

Затем (на втором этапе) на основе разработанной СФЦ и заданного логического критерия программный комплекс автоматически решает соответствующую систему логических уравнений и определяет логическую функцию надежности. Так, для рис. 9 .9 она имеет вид

(9.3)

Далее, на третьем этапе этот же комплекс автоматически преобразует полученную логическую функцию в "правильный" (точный) многочлен расчетной вероятностной функции. При предположении о независимости событий х₁ и х₂ она выражается уравнением

(9.4)

где – величина, дополняющая вероятность надежного срабатывания первого элемента этой системы до единицы.

На завершающем (четвертом) этапе программный комплекс выполняет (используя только что приведенный многочлен вероятностной функции) точный расчет искомой вероятностной характеристики системы. При этом (в нашем случае) оказывается, что вероятность ее безотказной работы

II. Прогнозирование показателей защищенности системы. Как и ранее (см. параграф 3.1), под защищенностью (структурной стойкостью или условной живучестью) подразумевается способность системы сохранять работоспособность после воздействия опасных факторов, возникающих при взрыве, пожаре или в иных нестандартных ситуациях, чреватых повреждением ее элементов. При этом условность живучести определяется достоверностью возникновения поражающих факторов, тогда как надежность элементов считается абсолютной.

Рис. 9.10. Схема функциональной целостности для защищенности системы

На первом этапе построения СФЦ для защищенности исследуемой здесь (см. рис. 9.8) системы будут использованы два новых случайных события х₃ и х₄, означающие независимое поражение ее элементов 1 и 2 достоверно возникшим поражающим фактором. В СФЦ защищенности, показанной на рис. 9.10, эти случайные события представлены функциональными вершинами 3 и 4. При этом поражение данных элементов достоверно возникшим поражающим фактором происходит с вероятностями р₃= 0,3 и р₄= 0,4 соответственно.

Условиями непоражения (сохранения работоспособности благодаря резистентости или стойкости) элементов 1 и 2 в данном случае будут уже инверсные исходящие дуги из показанных выше вершин 3 и 4. Условие соответствует также и исходящей дуге из имеющейся там фиктивной вершины 7 и является логическим критерием 7_с = у₇ защищенности исследуемой здесь системы в целом.

Результаты всех остальных этапов автоматического построения – вначале логической и вероятностной математических моделей, а затем формул для расчета защищенности (стойкости или условной живучести) данной системы по отношению к достоверно возникшим опасным фактором – принимают вид следующих логических и алгебраических уравнений:

а) логическая функция защищенности данной элементарной системы:

(9.5)

б) многочлен расчетной вероятностной функции защищенности исследуемой здесь системы:

(9.6)

где – параметры стойкости всех ее элементов;

в) вероятность защищенности (вероятность непоражения данной системы) оказалась равной

III. Прогнозирование безопасности (как дополнения интегрального показателя техногенного риска) осуществим с использованием

показанной на рис. 9.9 модели надежности, которую дополним тремя фиктивными вершинами, присвоив им цифровые коды 100, 70 и 30. Предположим также, что соответствующие им комбинации Y_oj отказов элементов моделируемой системы приводят к возникновению техногенных происшествий с конкретными разрушительными последствиями , оцениваемыми в условных единицах измерения ущерба:

(9.7)

СФЦ для оценки безопасности функционирования рассматриваемой здесь системы, полученная подобным способом, изображена на рис. 9.11.

Рис. 9.11. Схема функциональной целостности для безопасности системы

Приведенные входящие дуги узлов 100, 70 и 30, одновременно являющихся исходящими дугами из вершин 6 и 7, указывают логические условия возникновения различных исходов происшествия, тогда как исходящие дуги этих же узлов данной модели задают уже логические критерии всех этих нежелательных событий, характеризуемых различными последствиями для системы и имеющих вид математических зависимостей (9.7).

Автоматизированный расчет каждого параметра интегрального показателя техногенного риска с помощью технологии АСЛМ показал, что

Следует отметить, что СФЦ, примененная выше для прогнозирования уровня безопасности функционирования выбранной для примера системы по интегральному показателю техногенного риска, а также логические и вероятностные модели для происшествий с ущербом в 70 и 30 у.е. являются немонотонными, несмотря на то что исходная модель надежности была и остается монотонной по определению.

IV. В завершение рассмотрим прогнозирование показателей (полной, безусловной) живучести, под которой подразумевается способность системы сохранять (хотя бы частично) работоспособность при случайных поражениях ее элементов вследствие возникновения опасных факторов взрывов, пожаров и т.п. При этом надежность элементов, как и прежде, считается абсолютной, а для учета случайности поражающего фактора в разрабатываемую СФЦ вводится соответствующее событие х₅, появление которого эквивалентно воздействию и возможному поражению элементов 1 и (или) 2 системы, а непоявление – достоверному сохранению их работоспособности.

Путем дополнения ранее разработанной модели защищенности (см. рис. 9.10) функциональной вершиной 5 (возникновение поражающего фактора) и указанием на соответствующем графе дугой y₅ условий наступления событий х₃, х₄ (поражения элементов 1 и 2), получим СФЦ, пригодную уже для априорной оценки живучести рассматриваемой системы. Данная графическая модель и эквивалентные ей уравнения алгебры логики показаны на рис. 9.12.

Предположим также, что возникновение поражающего фактора происходит с вероятностью р₅ = 0,7, а вероятности р₃ = 0,3, р₄ = 0,4 являются параметрами уязвимости элементов 1 и 2 системы по отношению к этому фактору. Выход имеющейся в этой СФЦ фиктивной вершины 7 представляет условие у₇ =у₃ v y₄ сохранения работоспособности хотя бы одним из данных элементов, которое как раз и является критерием Y_ж =у₇ живучести (уже полной, а не условной – как для защищенности) системы при случайном возникновении и воздействии на нее поражающего фактора.

Рис. 9.12. Схема функциональной целостности для живучести системы

Результаты следующих трех этапов моделирования и расчета живучести, автоматически полученные с помощью программного комплекса "АРБИТР", представлены ниже:

а) логическая функция стойкости исследуемой здесь элементарной системы

(9.9)

б) расчетный многочлен соответствующей вероятностной функции

(9.10)

где – параметры стойкости элементов данной системы;

в) вероятностный показатель живучести ее функционирования .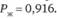

Следует отметить, что СФЦ для живучести исследуемой двухэлементной системы (см. рис. 9.12) также оказалась немонотонной по построению. Это означает, в частности, что подобная структурная модель живучести не может быть построена с помощью таких диаграмм влияния, как дерево происшествия. Вместе с тем полученные здесь логическая и вероятностная функции живучести еще остаются монотонными в рамках принятых содержательных определений используемых элементарных событий.

Как представляется, рассмотренные выше примеры иллюстрируют конструктивность использования общего логико-вероятностного метода и основанной на нем технологии АСЛМ для моделирования и расчета показателей таких наиболее важных свойств функционирования сложных систем, как надежность, защищенность, безопасность и живучесть. Правильность решения каждого примера несложно проверить вручную. Убедившись же в достоверности получаемых при этом результатов, правомерно применить изложенный здесь подход для постановки и решения более сложных и высокоразмерных задач, связанных с системным исследованием человекомашинных систем в целях прогнозирования техногенного риска.

На этом завершим знакомство с общими принципами ручного и автоматизированного прогнозирования параметров риска техногенных чрезвычайных ситуаций и приступим к более детальному рассмотрению того, как эти базовые руководящие положения могут реализовываться в процессе моделирования с помощью перечисленных выше диаграмм типа "дерево", "граф" и "сеть". Более конкретная информация о программном комплексе "АРБИТР", официально допущенном к подобному прогнозу рассматриваемых здесь показателей реальных технических систем, приведена в приложении Е.1 к данной книге.