Алгоритм планирования транспортировки
При решении задач по оперативному планированию доставки автомобильным транспортом основными экономико-математическими моделями являются транспортная задача и задача маршрутизации. Рассмотрим схемы организации доставки и применяемые методы планирования.
Первая схема организации доставки товаров является более простой с точки зрения планирования, так как вариант "один-к-одному" не предполагает решения ни транспортной задачи, ни задачи маршрутизации.
При планировании доставки товаров по схеме "один-ко-многим" необходимо решение задачи маршрутизации, которая включает в себя решение:
• задачи определения порядка выполнения маршрутов, при этом учитывается, что между отправителями и получателями перевозка осуществляется только по маятниковым маршрутам и транспортное средство в течение дня может выполнить несколько маятниковых маршрутов для разных получателей;
• задачи коммивояжера, если между отправителями и получателями перевозка осуществляется только по развозочным (сборным или сборно-развозочным) маршрутам;
• двух указанных выше типов задач, если при организации перевозочного процесса используются как маятниковые, так и развозочные (сборные или сборно-развозочные) маршруты.
Организация движения по третьей схеме ("многие-ко-многим") предполагает сначала решение транспортной задачи, а затем задачи маршрутизации перевозок.
Последовательность этапов планирования доставки товаров с учетом схем организации перевозочного процесса и применяемых методов представлена па рис. 8.2.
В качестве исходной информации (первый блок) в алгоритме используются данные о количестве транспортных средств, их типе, грузоподъемности (грузовместимости); количестве отправителей (поставщиков товаров) и получателей; партии перевозимого груза; временные ограничения по доставке товаров в пункты назначения и их вывозу из пунктов отправления. На основе имеющейся информации во втором блоке определяется схема организации перевозок (см. табл. 8.4).
Для дальнейших расчетов вычисляются кратчайшие расстояния от пункта (-ов) погрузки до пункта (-ов) разгрузки (четвертый блок, задача А), для этого используется база данных третьего блока алгоритма, представленного на рис. 8.2.
Задача вычисления кратчайшего пути из первого пункта маршрута в т-й сводится к выбору чисел х- ({,] =1,2,т), при которых достигается минимум функции, определяющей длину маршрута между начальным и конечным пунктами:

Для решения задачи считается, что длины участков пути между каждой парой соседних пунктов известны и равны а число = 1, если участок является звеном выбранного маршрута движения, и хі} = 0, если он не входит в этот маршрут. В качестве параметров при необходимости могут учитываться не только расстояния, но и время проезда по участкам дорожной сети, и стоимость перевозки по участку маршрута.
В пятом блоке, если используется схема "многие-ко-многим", решается транспортная задача. На этапе согласования схемы доставки определяется, но какому маршруту — маятниковому или развозочному (сборному или сборно-развозочному) — будет перевозиться товар от каждого поставщика к получателям, закрепленным за ним в результате решения транспортной задачи.
Экономико-математическая модель транспортной задачи выглядит следу ю щи м об разом:
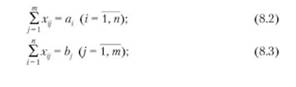
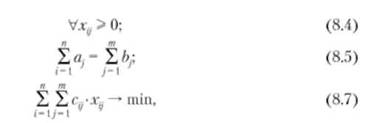
где г — количество поставщиков;; — количество потребителей; щ — ограничения по предложению; Ь-} — ограничения по спросу; — элементы целевой функции (расстояние, стоимость перевозки между грузообразующим
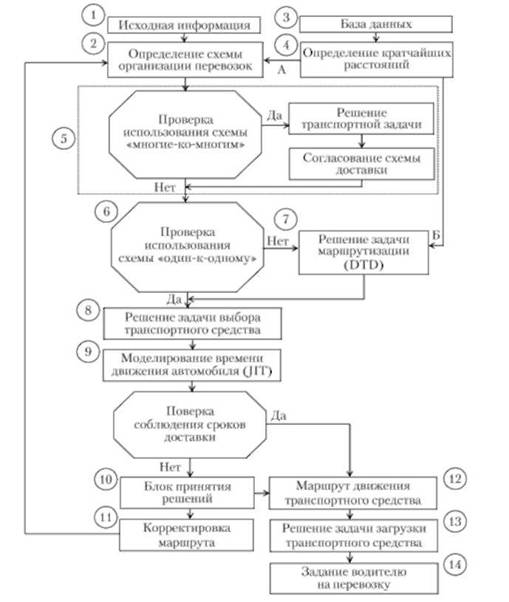
Рис. 8.2. Общий алгоритм планирования грузовых автомобильных перевозок
и грузопоглощающим пунктами); xtj — объем корреспонденции между г'-й и_/'-й точками.
Решение транспортной задачи находится с помощью специальных методов, позволяющих из множества возможных решений найти оптимальное. Одним из таких методов является распределительный метод, имеющий несколько разновидностей, которые отличаются способом определения оптимального решения. Наиболее распространены три разновидности данного метода: метод Хичкока; метод Креко; модифицированный распределительный метод, или метод потенциалов. Первоначальное допустимое решение также может быть получено несколькими способами. Наиболее простым является метод северо-западного угла. Для получения более приближенного к оптимальному плана перевозок рекомендуется использовать методы наименьшего элемента в матрице, метод двойного предпочтения, метод аппроксимации Фогеля.
Для решения транспортной задачи и определения кратчайших расстояний в настоящее время широко используются встроенные функции Microsoft Excel.
Исторический экскурс
Транспортная задача была впервые сформулирована в 1781 г. французским математиком Гаспаром Монжем. Больше всего для решения транспортной задачи было сделано в XX в. Исследования в данной области проводились как в Советском Союзе, так и в западных странах. В 1939 г. задача формирования национального плана перевозок, который позволил бы минимизировать суммарный километраж при организации доставки железнодорожным транспортом при наличии не более двух поставщиков, была предложена в Советском Союзе математиком А. Н. Толстым. Аналогичная задача в классическом виде была сформулирована в США Ф. Хичкоком примерно в это же время — в 1941 г. Метод последовательного улучшения, предложенный Ф. Хичкоком, получил название метода Хичкока. Большой вклад в развитие алгоритмов решения транспортной задачи привнес советский математик Леонид Витальевич Канторович. В период 1939—1949 гг. вышли в свет его работы, в которых предлагается решение задачи о перевозках. В частности, Л. В. Канторович и М. К. Гавурин, исследуя проблему рационализации грузопотоков, предложили метод потенциалов для решения транспортной задачи. В этот же период в США также исследуются методы решения транспортной задачи. Задача, сформулированная Ф. Хичкоком, была детально проработана Тьяллингом Чарльзом Кумпансом, который во время Второй мировой войны работал членом Объединенного комитета перевозок. Леонид Канторович и Тьяллинг Кумпанс, работая независимо друг от друга, нашли множество научных решений проблем экономики и в 1975 г. стали лауреатами Нобелевской премии в области экономики "за вклад в теорию оптимального распределения ресурсов".
Метод северо-западного угла для получения начального решения транспортной задачи был предложен в 1951 г. Джорджем Бернардом Данцигом, американским математиком, который вместе с Л. В. Канторовичем считается основоположником линейного программирования.
В шестом блоке проверяется наличие схемы "один-к-одному". Если по факту данной схемы нет, то в маршрут включается более одного грузоотправителя и (или) грузополучателя. Эта ситуация требует решения задачи маршрутизации (седьмой блок).
Математическая постановка задачи маршрутизации зависит от типа маршрута, по которому планируется осуществлять перевозку груза, а именно: по маятниковым или развозочному (сборному, сборно-развозочному). В первом случае решается задача определения порядка выполнения маршрутов, а во втором — задача коммивояжера. Дополнительной исходной информацией для рассматриваемых задач является матрица кратчайших расстояний между потребителями, поставщиками и автотранспортным предприятием (если доставка передана поставщику транспортных услуг), которая строится в четвертом блоке предложенного алгоритма (задача "Б"). Первоначальный перечень пунктов одного маршрута определяется исходя из совместимости грузов — для маятниковых маршрутов, и исходя из грузоподъемности транспортного средства — для развозочных (сборных или сборно-развозочных) маршрутов.
В восьмом блоке алгоритма решается задача выбора подвижного состава, соответствующего условиям перевозки и перевозимому грузу. Под выбором транспортного средства понимается определение его специализации и грузоподъемности с целью обеспечения минимальных затрат в цепи поставок товара.
При формировании маршрутов не был учтен случайный характер составляющих процесса доставки, количественная оценка вероятностного характера параметров перевозок может быть получена с использованием статистического моделирования (девятый блок). Моделирование времени движения транспортного средства на отдельных участках маршрута, времени погрузки и разгрузки, плановых и незапланированных простоев, перерывов и отдыха позволяет построить функцию распределения времени прибытия подвижного состава в пункты маршрута (пункт погрузки, разгрузки, пограничный переход, порт и др.). Моделирование времени маршрута позволяет оценить риски, связанные с обеспечением доставки точно в срок.
Исторический экскурс
Метод статистического моделирования (метод Монте-Карло) сегодня широко используется в разных сферах научных исследований. В логистике и управлении цепями поставок существует ряд задач, которые могут быть смоделированы на основе данного метода. Интересно, что, несмотря на то что первая работа по статистическому моделированию была опубликована в 1873 г. при организации стохастического моделирования для экспериментального определения числа к, годом рождения метода Монте-Карло считается 1949 г. Основателями метода считаются американские математики Стэнли Улам, Джон фон Нейман и Николас Метрополис. Благодаря их исследованиям изменился подход к статистическим испытаниям: если раньше моделирование нужно было для имитации решений детерминированных проблем с целью их проверки, то метод Монте-Карло научил исследователей находить стохастический аналог любых детерминированных явлений и ситуаций.
Название метода происходит от одноименного города, известного своими игорными домами, при этом авторы метода не имели к нему какого-либо отношения. Метод основывается на генерировании случайных чисел, а рулетка представляет собой "генератор" чисел, выпадающих совершенно случайно. Именно случайные числа объединяют город в княжестве Монако и метод статистического моделирования, что и стало причиной появления названия "метод Монте-Карло". Широкое распространение метода объясняется тем, что у него нет привязки к конкретному объекту или сфере деятельности, он универсален. Первые исследования проводились в ядерной физике, сегодня метод стал инструментом изучения во многих других сферах. Моделирование многократно ускоряется благодаря использованию компьютеров.
В десятом блоке рассматриваемого алгоритма определяется соотношение между смоделированными значениями времени прибытия в пункты маршрута с определенной вероятностью и требованиями потребителей по срокам доставки груза, временными ограничениями, вытекающими из самой схемы доставки (например, время прибытия на паромную переправу или к открытию магазина). Если смоделированное значение времени доставки окажется больше ограничения (требования потребителя), необходимо принять решение о возможности и целесообразности организации дополнительного маршрута, корректировки условий выполнения заказа, маршрута движения или внесения других изменений, чтобы максимально удовлетворить требования потребителей (одиннадцатый блок).
В случае принятия решения о корректировке разработанного или организации дополнительного маршрутов, требуется повторить выполнение алгоритма со второго по одиннадцатый блок.
При соблюдении сроков доставки по результатам моделирования получаем оптимальные маршруты движения каждого транспортного средства (двенадцатый блок), позволяющие с минимальными затратами полностью удовлетворить требования потребителей.
Далее для всех полученных маршрутов в тринадцатом блоке необходимо решить задачу загрузки транспортного средства. Математическая постановка известна только для задачи о "рюкзаке" или "ранце", в которой качество загрузки транспортного средства обычно оценивается таким показателем, как количество транспортных средств, используемых для перевозки заданных объемов грузов, что оправданно при организации массовых перевозок. Перевозка различных мелкопартионных грузов требует составления развозочного маршрута, в результате появляется новое условие в оценке качества загрузки транспортного средства, а именно: рациональная загрузка кузова подвижного состава исходя из порядка объезда пунктов на маршруте. Самое простое решение — сформировать заказ каждого клиента на отдельном поддоне, тогда погрузка транспортного средства начинается с заказа последнего клиента. Если груз у грузоотправителя хранится и загружается в подвижной состав по наименованиям, такая задача не имеет в настоящее время оптимального решения.
В результате реализации алгоритма может быть получено задание водителю на рейс (день), в котором отражается количество груза, предъявляемое к перевозке от отправителей получателям, порядок объезда пунктов на маршруте, временные интервалы выполнения перевозки.
Выводы
1. Какие задач выполняет транспортировка в цепях поставок?
Поскольку производители (поставщики) и потребители находятся на расстоянии друг от друга, возникает потребность участников цепи поставок в доставке поставляемых товаров. При этом транспортировка выполняет не только физически связывающую поставщиков и потребителей функцию, но и обеспечивает достижение целей логистики в целом, а именно: транспортировка должна быть организована так, чтобы обеспечить снижение общих логистических издержек, повышение качества обслуживания потребителей, ускорение логистических циклов как в отдельных областях логистики, так и в целом по цепи поставок. Выбор наилучших решений и технологий доставки для достижения данных целей является основным предназначением транспортировки в цепях поставок.
Задачи транспортировки подразделяются на технологические, аналитические, задачи выбора наилучших решений, задачи управления объектами логистической инфраструктуры (в части транспортных объектов).
2. Что понимается под выбором вида транспорта и способа транспортировки?
Выбор способа транспортировки и вида транспорта — это связанные задачи. Сначала определяется способ транспортировки, т.е. принимается решение о том, одним видом транспорта или несколькими будет выполняться доставка. Затем выбираются виды транспорта под способ транспортировки с учетом особенностей конкретных видов транспорта, требований к параметрам доставки, естественно-географическими условий выполнения перевозок, характера товара как груза, возможности выбора специализированного транспорта, традиций и уровня развития экономических отношений между участниками цепи поставок.
3. На основании каких критериев осуществляется принятие решений в транспортировке?
Основными критериями выбора в транспортировке являются стоимость доставки, время, затрачиваемое на перевозку, качество доставки, выполнение сопутствующих услуг и др.
4. Какие условия выполнения доставки учитываются при управлении транспортировкой?
Помимо обеспечения выполнения доставки по параметрам стоимости, времени и качества учитываются технологические особенности выполнения перевозки товаров. Прежде всего, это технологическая схема ("один-к-одпому", "один-ко-многим", "многие-ко-многим"), которая определяет возможные варианты организации маршрутов. Маршрут — это путь следования транспортного средства. Например, на автомобильном транспорте выполняются маятниковые и кольцевые (в том числе развозочные, сборные, сборно-развозочные) маршруты.
В управлении транспортировкой важным является обеспечение доставки к точно указанному сроку, поэтому результаты моделирования доставки также учитываются при организации перемещения товаров в цепи поставок.