Алгоритм имитационного моделирования процесса появления происшествий на основе сети GERT

Приемлемость метода имитационного моделирования для априорной оценки меры возможности появления техногенных происшествий может быть обоснована по меньшей мере двумя соображениями. Во-первых, выполнение большинства проводимых на ОТУ операций удобно представлять в виде процесса функционирования какой-либо человекомашинной системы. При этом успешное или неуспешное завершение каждой такой операции будет случайным исходом – соответственно непоявлением или появлением в ней техногенного происшествия. Во-вторых, если же рассматривать конкретную технологическую операцию, многократно выполняемую на однотипных ОТУ, то можно утверждать и о массовом характере интересующих нас исходов.

Следовательно, требование к массовости и стохастичности исследуемого процесса соблюдается, что позволяет использовать метод имитационного моделирования для прогнозирования рассматриваемого здесь параметра аварийности и травматизма. Для пояснения идеи имитационного моделирования техногенных происшествий в человекомашинной системе обратимся к рис. 12.3, где рассмотренная выше семантическая модель представлена уже в виде "чистой" сети стохастической структуры типа GERT. Эта сеть содержит узлы и дуги, которые в построенном на ее основе машинном алгоритме будут определять условия генерирования, обработки или передачи потока цифровой информации, указывающей на вклад учитываемых при моделировании факторов аварийности и травматизма.

Для удобства восприятия источники такой информации (генераторы случайных чисел, представляющие свойства человекомашинной системы) помечены волнистыми стрелками, входящими в соответствующие узлы сети GERT, а все ее узлы и некоторые дуги – цифрами, часть из которых уже использована в предыдущей модели (см. рис. 12.2). При этом все узлы данной сети имеют одинаковые (единичные) степени свободы для первой и последующих реализаций (в смысле приема сигнала, поступающего от входящих дуг).

Кроме того, только три узла этой сети 23, 33 и 35 имеют более двух исходящих дуг. На рис. 12.2 они соответствовали выполнению человеком следующих этапов операторского алгоритма:

а) восприятие и дешифровка информации о состоянии человеко-машинной системы;

б) принятие решения о необходимости и порядке устранения причин нарушенного в ней равновесия;

в) практическая реализация оператором принятого решения.

Обратим внимание также на события, закодированные числами 26,44, 50, 64, 65, 78, 79 и оснащенные спиралевидными исходящими стрелками: при моделировании они будут играть роль узлов-статистик, т.е. регистрировать факт достижения всех этих событий потоком цифровой информации.

Исходными данными, необходимыми для имитационного моделирования, служит набор тех свойств человекомашинных систем (см. параграф 6.2), которые наиболее значимо влияют на появление техногенных происшествий, а также относительные оценки качества каждого такого фактора и его вклада в появление и развитие причинной цепи соответствующих предпосылок. Распределение качества всех учитываемых свойств-факторов этой системы будет задаваться при моделировании плотностью f_x(K) вероятности или функцией п_х(К) принадлежности соответствующих лингвистических переменных (см. параграф 2.2).

Что касается способов представления тех исходных данных, которые имеют нечетко определенную природу и используются при моделировании, то они задаются с помощью универсальной шкалы, приведенной в табл. 12.2.

Таблица 12.2. Лингвистические и числовые оценки универсальной шкалы качества

Относительная и четырехбалльная оценки	Лингвистическая оценка
	Очень, очень низкое(К1)	Очень низкое (К2)	Низкое (КЗ)	Ниже среднего (К4)	Среднее (К5)	Выше среднего (Кб)	Хорошее (К7)	Очень хорошее (К8)	Высокое (К9)	Очень высокое (К10)	Очень, очень высокое (К11)
K Î [0; 1]	0,08	0,17	0,25	0,33	0,41	0,5	0,58	0,66	0,75	0,83	0,92
Плохо	0,3	0,7	1,0	0,7	0,3	0	0	0	0	0	0
Удовлетворительно	0	0	0,3	0,7	1,0	0,7	0,3	0	0	0	0
Хорошо	0	0	0	0	0,3	0,7	1,0	0,7	0,3	0	0
Отлично	0	0	0	0	0	0	0,3	0,7	1,0	0,7	0,3

Для пояснения механизма имитационного моделирования происшествий в человекомашинной системе обратимся к рис. 12.4.

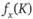Ломаной линией (а) на этом рисунке показана треугольная функция принадлежности оценки "хорошо", а прямой (б) – равномерно распределенная плотность вероятности качества двух взятых для примера свойств этой системы (факторов аварийности и травматизма). Их вклад в появление и развитие причинной цепи техногенного происшествия зависит от присвоенных оценок качества и индекса 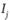потенциальной опасности. При этом величина последнего может определяться с помощью статистических данных по аварийности и травматизму (например, по процентному распределению соответствующих факторов, приведенных на рис. 6.4). В частности, найденные подобным образом значения этих индексов приведены в табл. 12.3 совместно с кодами и наименованиями каждого учтенного в модели фактора-свойства человекомашинной системы.

Сущность идеи, положенной в основу имитационного моделирования происшествий в человекомашинных системах, состоит в следующем. Генераторы случайных чисел (см. левую часть рис. 12.4), настроенные на равномерно или треугольно распределенные функции I и , выдают при опросе случайные оценки качества, значения которых влияют на индексы потенциальной опасности. Количество таких генераторов соответствует числу учитываемых факторов, а выданные ими значения индексов потенциальной опасности могут имитировать предрасположенность конкретных свойств человекомашинной системы к формированию предпосылок к происшествию.

В самом деле, если качество компонентов конкретной системы имеет низкие оценки, то генераторы чаще будут выдавать максимальные величины соответствующих случайных чисел-индексов: чем ниже оценка К. качества какого-либо свойства человекомашинной системы, тем наиболее вероятно принятие этим числом наибольшего значения индекса, приведенного в правой колонке табл. 12.3. А так как все свойства связаны между собой дугами сети GERT, то результат обработки этой цифровой информации ее узлами логического сложения и перемножения будет характеризовать возможность появления и развития причинной цепи предпосылок к техногенному происшествию.

Рис. 12.3. Сеть GERT для имитационного моделирования происшествий

Рис. 12.4. Иллюстрация механизма имитационного моделирования

Таблица 12.3. Состав и характеристика учитываемых факторов

Компонент	Код	Наименование моделируемых факторов	Номер узла		Индекс Ij
			исток	сток
Человек	Ч1	Наличие практических навыков выполнения операции	5	6	1 ˅ 0
	Ч2	Знание технологии работ на данном оборудовании	7	8	2 ˅ 0
	Ч3	Пригодность по психофизиологическим показателям	9	10	1 ˅ 0
	Ч4	Восприятие и дешифровка информации о состоянии системы	23	24	1 ˅ 2 ˅ 3 ˅ 0
	Ч5	Оперативность мышления человека-оператора	27	28	1 ˅ 0
	Ч6	Знание порядка действий в нестандартных ситуациях	29	30	1 ˅ 0
	Ч7	Способность прогнозировать последствия своих решений	31	32	1 ˅ 0
	Ч8	Технологическая дисциплинированность	57	58	2 ˅ 0
	Ч9	Качество принятия решения	33	34	1 ˅ 2 ˅ 0
	Ч10	Знание опасных факторов выполняемой операции	59	60	1 ˅ 0
	Ч11	Осведомленность о последствиях аварийных ситуаций	41	42	1 ˅ 0
	Ч12	Знание порядка действий в аварийных ситуациях	39	40	1 ˅ 0
	Ч13	Обученность действиям в аварийных ситуациях	37	38	2 ˅ 0
	Ч14	Точность действий по ликвидации аварийных ситуаций	35	36	2 ˅ 1 ˅ 0
	Ч15	Безошибочность действий в критических ситуациях	69	70	2 ˅ 0
Машина	М1	Качество конструкции рабочего места человека-оператора	11	12	1 ˅ 0
	М2	Степень учета особенностей работоспособности человека	13	14	2 ˅ 0
	М3	Безотказность контрольно-измерительных приборов	21	22	1 ˅ 0
	М4	Энергоемкость источников опасных техногенных факторов	45	46	2 ˅ 0
	М5	Безотказность элементов, удерживающих опасные факторы	53	54	2 ˅ 0
	М6	Длительность действия опасных производственных факторов	55	56	1 ˅ 0
	М7	Уровень потенциала опасных производственных факторов	71	72	1 ˅ 0
	M8	Безотказность технических средств защиты и безопасности	75	76	2 ˅ 0
Среда	С1	Комфортность среды по физико-химическим параметрам	1	2	1 ˅ 0
	С2	Качество информационной модели состояния среды	3	4	2 ˅ 0
	С3	Возможность неблагоприятных воздействий среды на систему	19	20	1 ˅ 0
	С4	Возможность нерасчетных внешних воздействий на систему	47	48	2 ˅ 0
Технология	Т1	Удобство подготовки и выполнения работ на технике	15	16	1 ˅ 0
	Т2	Удобство технического обслуживания и ремонта оборудования	17	18	2 ˅ 0
	Т3	Сложность алгоритмов функционирования человека-оператора	51	52	1 ˅ 0
	Т4	Возможность появления персонала в опасной зоне	61	62	1 ˅ 0
	Т5	Возможность появления в опасной зоне других незащищенных элементов	67	68	1 ˅ 0
	Т6	Надежность организационно-технических средств обеспечения безопасности	73	74	2 ˅ 0

Ведь нетрудно понять, что обработка логическими узлами значений 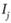будет формировать суммарный индекс потенциальной опасности моделируемого процесса, а его величина может указывать на возможность образования причинной цепи происшествия в человекомашинной системе. Это будет определяться не только случайно выбранными в конкретной реализации значениями отдельных , но также логикой их сложения и перемножения, заданной соответствующими узлами той сети GERT, которая представлена на рис. 12.3.

В свою очередь, полученная таким образом величина 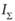может указывать на предрасположенность исследуемой системы к происшествиям, оцениваемую вероятностями не только возникновения возмущений, опасных и критических ситуаций, но и ее адаптации вследствие их своевременной ликвидации. Последнее объясняется тем, что случайная величина , значение которой пропорционально вероятности образования причинной цепи техногенного происшествия, способна не только расти, но и уменьшаться, вплоть до обнуления.

Например, сохранение или рост индекса будет иметь место после объединения логическим условием ИЛИ поступающих на его вход случайных чисел . Допустим, при алгебраическом сложении соответствующего вклада тех первых девяти узлов-генератооов сети GERT, которые соответствуют факторам с кодами 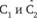., , , 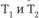. И напротив, уменьшение , т.е. обрыв причинной цепи техногенного происшествия, будет интерпретироваться в тех случаях, когда хотя бы один из генераторов, инцидентных логическому условию И, выдаст нулевое значение индекса . Например, когда узлы 23, 24 этой сети (фактор 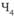) сымитируют безошибочное восприятие и дешифровку информации оператором, несмотря на ненулевые значения индексов и

Естественно, что каждая машинная реализация конкретной технологической операции будет сопровождаться регистрацией одного из тех событий, которые помечены в левой и правой частях рис. 12.3 исходящими из них волнистыми стрелками. Это означает, что в одних случаях в исследуемой человекомашинной системе (ЧМС) может фиксироваться гомеостазис или адаптация к возникшим ошибкам, отказам и нерасчетным внешним воздействиям, а в других – опасная и критическая ситуации, т.е. достижение узлов 26, 44 и 50, 65 потоком цифровой информации. Если последующие значения индекса накопленной опасности не превысят некоторых предельных значений, то в моделируемой системе будет регистрироваться адаптация и к этим ситуациям (узлы 64 и 78), тогда как дальнейший рост может завершиться уже техногенным происшествием – появлением одного из событий 79а, 796 или 79в в верхней части рис. 12.3.