Закон убывающей полезности благ

По мере достижения некоего максимума насыщения потребности данным благом его полезность для покупателя начинает снижаться. Это происходит потому, что каждая дополнительная единица последующих покупок данного блага приносит потребителю относительно меньшее удовлетворение, чем предыдущие. Применительно к каждой единице покупок существует некий предел, достигая которого, значимость полезных свойств одних и тех же покупок начинает снижаться, убывать. Математическую интерпретацию процесса насыщения субъективных потребностей людей в экономических благах дал немецкий экономист Герман Генрих Госсен (1810—1858). Открытые и доказанные им особенности данного субъективного процесса в сфере товарных покупок получили название первого закона Госсена, или закона убывающей предельной полезности благ (см. 24.1).

Предельная полезность — MU (от англ. marginal utility) — это полезность, которую приносит потребителю использование дополнительной единицы данного блага. Этот гипотетический измеритель в теориях кардинализма выступает своеобразным критерием субъективно определяемой потребителем ценности полезных свойств экономических благ. Принято считать, что в количественном выражении это величина полезного эффекта для потребителя от осуществленной им покупки дополнительной единицы одного и того же блага. Величина этого полезного эффекта может быть ничтожно мата, но ее наличие увеличивает общую (суммарную) полезность покупок данного блага. Приращение покупателем полезности выражается в дополнительных покупках экономических благ, которые удовлетворяют запросы и потребности, а следовательно, приносят соответствующий полезный эффект. Ведь суммарный полезный эффект от потребления двух, или трех, или четырех и последующих единиц товара выше, чем от одной единицы товара, имеющего необходимые покупателю потребительские свойства. Однако при возрастании суммарного эффекта полезности одновременно происходит и неуклонное убывание предельной полезности каждой последующей дополнительной единицы одноименного блага. В этом смысле показателен классический пример утоления жажды: удовлетворение от первого стакана воды большее, чем от второго, третьего и т.д.; наконец, в дальнейшем в потреблении воды просто нет необходимости. Таким образом, суть экономического закона убывающей предельной полезности состоит в том, что по мере приращения суммарного полезного эффекта от потребления блага неуклонно убывает предельная полезность каждой дополнительной единицы этого приращения. Закон убывающей предельной полезности можно представить в виде таблицы с условным числовым примером (табл. 7.1).

Таблица 7.1. Числовой пример убывающей предельной полезности благ

Количество благ, единиц	Суммарный полезный эффект	Предельная полезность благ
0	—	—
1	4	4
2	7	3
3	9	2
4	10	1
5	10	0

Приращение количества экономических благ (гр. 1) от нуля до пяти единиц сопровождается увеличением суммарного полезного эффекта (гр. 2).

Однако значения предельной полезности каждой дополнительной единицы приращения благ (гр. 3) неуклонно снижаются и при достижении пятой единицы равняются нулю. Предельная полезность благ определяется как разность величин последующего и предыдущего числового значения суммарного полезного эффекта (гр. 2). При пулевой предельной полезности блага (в нашем примере это пятая единица) его дальнейшее приращение экономически нецелесообразно. Представленный в нашей таблице закон убывающей предельной полезности может быть записан в виде функции общей полезности:

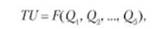
где Тії — суммарный полезный эффект; ()ґ 0^(X — блага (от одного до пяти), потребляемые покупателем.

Предельная полезность — это частная производная от общей суммарной полезности последовательно приобретаемых благ. Применительно к нашему числовому примеру она имеет следующий вид:

где возрастание суммарного полезного эффекта в процессе приращения благ имеет вид убывающей функции, как показано па рис. 7.1.

Первый закон Госсена, или закон убывающей предельной полезности благ, может быть показан также в виде графиков. Рост суммарного полезного эффекта постепенно убывает и прекращается в интервале от четвертой до пятой единицы приращения, где достигнутый суммарный эффект десяти единиц не изменяется, что делает экономически бессмысленным и неэффективным процесс дальнейших покупок данного блага. Рис. 7.2

Рис. 7.1. Функция суммарного полезного эффекта

Рис. 7.2. Функция убывающей предельном полезности

иллюстрирует функцию убывающей предельной полезности каждой дополнительной единицы приращения от нуля до пяти единиц. Динамика и темп этого убывания являются зеркальным отражением функции суммарного полезного эффекта: каждая поВперед единица блага, дающая его приращение, выражается соответствующим убыванием предельной полезности приращения.

Второй закон Госсена представляет собой интерпретацию потребительского поведения с учетом субъективно оцениваемой покупателем предельной полезности собственных денег, предназначенных для покупок. Действие закона убывающей предельной полезности распространяется и на такое экономическое благо, как деньги вообще (М) и денежный доход потребителя, его личный бюджет, направляемый на закупку благ индивидуального пользования, в частности. Цены потребительских благ — это внешнее и наиболее общее денежное выражение содержащегося в них полезного эффекта. Гипотетическая единица измерения этой полезности — ютиль — обретает реальное выражение в соответствующих денежных единицах, именуемых ценой. Цены потребительских благ нс зависят от покупателя, который свободен в своем выборе и предпочтениях, товарные дефициты отсутствуют, и единственным ограничителем выступает лишь сумма денег для покупок. Ограниченность денег, дохода, личного бюджета позволяет (и вынуждает) гипотетические штили полезного эффекта любого товара представить в денежном выражении, адекватном размерам собственных денежных возможностей для покупок. Именно по этой причине потребитель всегда сопоставляет не только полезные эффекты покупаемых товаров, но и сравнивает их с полезностью собственных денег. Это можно представить следующим образом:

где МГУ,, ...,Миш1 — предельная полезность покупаемых благ; Р{, „в,Ря — цена покупаемых благ; X — предельная полезность денег.

Приложение. Функция Лагранжа и максимизация полезности

Решение задачи по максимизации функции полезности

У = Щ01 0.? - 0,,) так - при бюджетном ограничении;

М = Р, £), + Р20,2 + + Р„0,' где ^ ~ величина бюджета, может быть сведено к максимизации функции Лагранжа:

I = ^(СД,(£,) + X + Р.Д2 + ... + Р& - М), где X - сомножитель Лагранжа.

Первое слагаемое функции Лагранжа — это целевая установка потребителя по максимизации полезности приобретаемых благ; второе слагаемое функции — часть бюджета, израсходованная потребителем на эти блага. Сомножитель Лагранжа к в данном случае характеризует предельную полезность денег, расходуемых из личного бюджета на приобретенные блага.

Из условий достижения максимума функции

следует, что потребитель при заданных ценах и бюджетных возможностях достигает цели максимизации полезности осуществленных затрат, если отношение предельной полезности приобретенных благ к их цене одинаково и равно предельной полезности израсходованных денег, т.е.

где и = 811/ 3 0, — предельная полезность /'-го блага; х = А спросу на (I, который находится в прямой зависимости от М (бюджетных возможностей покупателя) и обратной зависимости от Р (цен покупаемых благ).