Выявление сезонности

Ознакомившись с типами сезонности, рассмотрим, как можно выявить сезонность в ряде данных.

Выводы о наличии либо отсутствии сезонности можно сделать на основе одного из трех методов:

1. Экспертный метод считается самым простым из трех методов и сводится к тому, что исследователь во время изучения объекта исследования заключает, что в анализируемом показателе, скорее всего, есть сезонность. Это умозаключение обычно следует из самой постановки задачи. Например, если приходится работать с квартальными данными по продажам мороженого, то можно ожидать, что в этих данных будет проявляться сезонность (второй и третий кварталы – рост, первый и четвертый – спад), следовательно, лаг сезонности будет равен 4. В дневных данных по посещаемости новостного сайта можно ожидать лаг сезонности, равный 7 (например, каждое воскресенье может происходить спад, так как люди отдыхают и им не до новостей).

К сожалению, этот метод не идеален, и в эволюционных процессах такое априорное предположение о наличии сезонности может не выполняться в связи с постоянным изменением структуры ряда и возможной сложной структурой сезонных колебаний (когда одни колебания накладываются на другие).

В целом можно заключить, что экспертный метод позволяет определить наличие сезонности в достаточно сложных ситуациях, но не всегда дает однозначные результаты.

2. Графический метод предполагает построение линейного графика по исследуемому показателю, на котором по оси абсцисс откладывается время наблюдения, а по оси ординат – значение показателя. На рис. 6.5 представлен график по части ряда № 2568, рассматривавшегося нами ранее. По нему видно, что каждый апрель наблюдается резкий скачок показателя, а каждый май – спад. Кроме того, сезонная структура явно прослеживается из года в год: каждый год в некоторые месяцы наблюдается спад, а в другие – рост относительно общего тренда. На основе такого графического анализа можно заключить, что ряд является сезонным, с лагом s=12.

Иногда для более точного выявления сезонности исходный ряд данных стоит предварительно сгладить простыми скользящими средними невысокого порядка (например, 3–6-го порядка для месячных данных). Делается это для того, чтобы избавиться от ошибок и увидеть трендовую и сезонную составляющие. В таком случае графический анализ может упроститься.

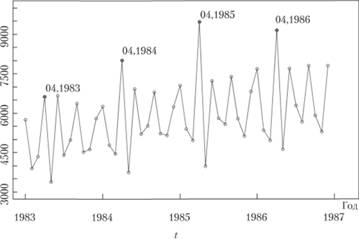
Рис. 6.5. Графическое представление ряда № 2568 из базы рядов М3

Однако не все сезонные ряды имеют такую явную структуру, как рассмотренный нами ряд № 2568. В связи с эволюционной сущностью многих экономических показателей меняться во времени может не только тренд, но и сезонные компоненты, из-за чего, например, пик продаж в разные годы может приходиться на разные месяцы. Поэтому графический метод не всегда позволяет однозначно выявить сезонность и может быть использован лишь в самых простых случаях.

3. Аналитический метод выявления сезонности заключается в построении коррелограммы исходного ряда данных и оценке значимости коэффициентов автокорреляции и частной автокорреляции. Существуют следующие индикаторы, сигнализирующие о наличии сезонности в исходном ряде данных:

• коэффициент автокорреляции оказывается значимым на лаге выше третьего порядка, что указывает на наличие сезонности данного порядка;

• коэффициент частной автокорреляции оказывается значимым на лаге выше третьего порядка, что также указывает на наличие сезонности данного порядка либо порядка, следующего за данным лагом;

• АКФ затухает по синусоиде;

• ЧАКФ затухает по синусоиде.

На рис. 6.6 показана коррелограмма для ряда № 2568 из базы М3, к которой мы уже обращались ранее в параграфе 5.1.

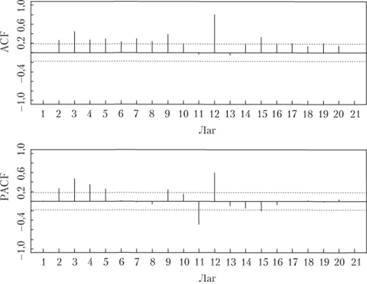
Рис. 6.6. Коррелограммы по автокорреляционной и частной автокорреляционной функциям для ряда № 2568 из базы рядов М3

Как видим, коэффициент автокорреляции на 12-м лаге оказался не только значимым, но еще и значительно больше по величине соседних коэффициентов. Коэффициенты частной автокорреляции на 11-м и 12-м лагах так же оказались значимыми. Это указывает на наличие сезонности в исследуемом ряде данных.

К сожалению, на практике по коррелограмме не всегда можно однозначно определить сезонность в ряде данных. В качестве примера па рис. 6.7 приведена коррелограмма по ряду данных № 1405 из базы рядов М3.

По рис. 6.7 видно, что автокорреляционная функция затухает с небольшими синусоидальными колебаниями: снижение на 7-м лаге сменяется повышением на 8-м, то же самое происходит с 3-м и 4-м, с 10-м и 11-м лагами и т.д. Такое поведение может сигнализировать и о наличии сезонности в исходном ряде данных, однако выраженной достаточно слабо. Вызвано это, скорее всего, тем, что исходный ряд имеет нестационарный характер. А раз так, то его перед дальнейшим анализом нужно привести к стационарному виду. Подробнее инструменты приведения к стационарности мы рассмотрим в параграфе 8.2,

Рис. 6.7. Коррелограммы по автокорреляционной и частной автокорреляционной функциям для ряда № 1405 из базы рядов М3

посвященном авторегрессиям. Пока же лишь заметим, если четко определить сезонность по коррелограммам не удается, имеет смысл изучить коррелограмму по разностям исходного ряда.

В целом можно сделать вывод, что при определении наличия сезонности и соответствующего ей лага стоит использовать комбинацию из упомянутых трех методов: вначале попытаться оценить ряд экспертно, затем построить график, после чего – коррелограмму по ряду. Такой подход поможет более точно выявить сезонность и определить лаг сезонности в любом ряде данных, в котором она действительно есть.

Теперь, когда мы разобрались, в чем именно заключается разница в учете сезонности аддитивно и мультипликативно, а также показали, как выявлять и идентифицировать сезонность, мы можем перейти к описанию различных методов декомпозиции временны́х рядов и построения тренд- сезонных моделей. Стоит отметить, что все существующие методы сезонной декомпозиции так или иначе сводятся к тому, чтобы для начала исключить из исходного ряда и ошибки, и сезонные компоненты, после чего оценить тренд, а уже затем вычислить сезонные коэффициенты. Поэтому методы и называются декомпозиционными, позволяющими заменить решение одной большой задачи решением серии меньших, более простых, взаимосвязанных задач.