Устойчивость сжатых стержней
Рассмотрим условия равновесия шарика (рис. 2.44, а – в). Если шарику дать малое отклонение в горизонтальном направлении, то в первом случае он вернется в исходное положение (состояние устойчивое), во втором – не вернется (неустойчивое положение), а в третьем случае откатится в сторону и остановится (положение безразличного равновесия). Аналогичные явления наблюдаются и в упругих телах.

Рис. 2.44
Пусть стержень нагружен продольной силой f (рис. 2.45). Приложим к стержню малую боковую силу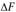 и снимем ее. Как и в случаях с шариком (см. рис. 2.44), после снятия нагрузки стержень может: 1) вернуться в исходное положение; 2) не вернуться в исходное положение; 3) остаться искривленным, т.е. упругий стержень может иметь три состояния: устойчивое, неустойчивое и безразличное состояние равновесия. Эти три положения, однако, здесь существенно зависят от силы F и геометрических размеров стержня. Аналогичные явления наблюдаются и во многих тонкостенных упругих системах, оболочках, пластинах и др. При некотором значении силы F. называемом критическим
и снимем ее. Как и в случаях с шариком (см. рис. 2.44), после снятия нагрузки стержень может: 1) вернуться в исходное положение; 2) не вернуться в исходное положение; 3) остаться искривленным, т.е. упругий стержень может иметь три состояния: устойчивое, неустойчивое и безразличное состояние равновесия. Эти три положения, однако, здесь существенно зависят от силы F и геометрических размеров стержня. Аналогичные явления наблюдаются и во многих тонкостенных упругих системах, оболочках, пластинах и др. При некотором значении силы F. называемом критическим , стержень нс распрямится, а сохранит искривленное положение, т.е. безразличное состояние равновесия. При незначительном превышении критической силы стержень начнет сильно искривляться и разрушаться. Допускаемая величина продольной силы
, стержень нс распрямится, а сохранит искривленное положение, т.е. безразличное состояние равновесия. При незначительном превышении критической силы стержень начнет сильно искривляться и разрушаться. Допускаемая величина продольной силы
 (2.96)
(2.96)
где 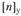 – запас устойчивости, который часто задается примерно равным запасу прочности по отношению к пределу текучести:
– запас устойчивости, который часто задается примерно равным запасу прочности по отношению к пределу текучести: 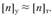
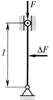
Рис. 2.45
Критическое напряжение сжатого стержня может быть и меньше предела упругости, и больше.
может быть и меньше предела упругости, и больше.
Впервые задача устойчивости сжатого стержня была решена Л. Эйлером в 1744 г. Он вывел формулу критической силы для длинных стержней, работающих в пределах упругости, из рассмотрения криволинейной формы равновесия стержня при постоянной нагрузке. Формула Эйлера имеет вид
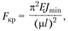 (2.97)
(2.97)
где Е – модуль упругости материала; – минимальный момент инерции сечения стержня;
– минимальный момент инерции сечения стержня;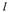 – длина стержня;
– длина стержня;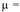
 – коэффициент приведения длины стержня, зависящий от числа полуволн п искривленного стержня, в свою очередь зависящих от вида закрепления стержня (рис. 2.46).
– коэффициент приведения длины стержня, зависящий от числа полуволн п искривленного стержня, в свою очередь зависящих от вида закрепления стержня (рис. 2.46).

Рис. 2.46
Вычислим по формуле Эйлера критические напряжения:
 (2.98)
(2.98)
Принято обозначать, где – радиус инерции сечения.
– радиус инерции сечения.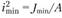
Тогда формула (2.98) принимает вид
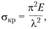 (2.99)
(2.99)
где  – гибкость стержня.
– гибкость стержня.
Если обозначить значение гибкости стержня, при котором критическое напряжение достигает предела упругости
значение гибкости стержня, при котором критическое напряжение достигает предела упругости  , то из формулы (2.99) получим
, то из формулы (2.99) получим
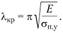 (2.100)
(2.100)
Формула Эйлера применяется в пределах упругости материала стержня , т.е. для гибкостей, бо́льших критических
, т.е. для гибкостей, бо́льших критических  .
.
Устойчивость стержней за пределами упругости
Для каждого материала можно построить график критических напряжений  , пользуясь механическими характеристиками материала.
, пользуясь механическими характеристиками материала.
График критических напряжений (рис. 2.47) имеет три области:
I – область пластических деформаций, в которой работают короткие стойки (стержни) на сжатие. Здесь потери устойчивости не происходит и за  принимается
принимается 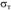 ;
;
II – область упруго-пластических деформаций. Критические напряжения в этой области определяются по формуле Ясинского (уравнения прямой линии):
 (2.101)
(2.101)
где а\b – коэффициенты уравнения прямой линии.
Так как прямая А В соединяет точки А и В, то, подставив координаты точек Л и В в уравнение (2.101), получим коэффициенты а и b;
III – область упругих деформаций – область Эйлера. Здесь определяется, по формуле Эйлера, выраженной в напряжениях (2.99).
определяется, по формуле Эйлера, выраженной в напряжениях (2.99).
Рассмотрим задачи на определение критических напряжений.
Задача 2.1. Задана стойка по форме и размерам. Известен материал. Требуется найти критическую нагрузку.
Задачу можно решить с помощью кривой критических напряжений. В любом случае определяем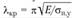 , затем
, затем  . Далее находим гибкость стойки
. Далее находим гибкость стойки по вычисленному ранее минимальному радиусу инерции
по вычисленному ранее минимальному радиусу инерции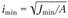 . При этом значения
. При этом значения и А берут из таблиц или вычисляют.
и А берут из таблиц или вычисляют.
По найденной гибкости устанавливают, в какой области работает стойка, и в зависимости от этого определяют  по со-
по со-
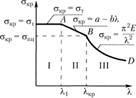
Рис. 2.47
ответствующей формуле для σκρ или по графику. Найдя , определяют
, определяют . Если задан запас устойчивости, находят допустимую нагрузку по формуле (2.96).
. Если задан запас устойчивости, находят допустимую нагрузку по формуле (2.96).
Задача 2.2. Известны предельная допустимая сила и запас устойчивости ,, т.е. известна
,, т.е. известна . Даны конструкция стойки, се материал. Требуется определить размеры сечения.
. Даны конструкция стойки, се материал. Требуется определить размеры сечения.
Эта задача – неопределенная, так как нельзя найти  , где
, где 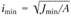 , поскольку
, поскольку  и А неизвестны.
и А неизвестны.
В этом случае задаются размерами сечения и решают прямую задачу (тип первый). Определяют значение и сравнивают с заданным. Если полученное значение
и сравнивают с заданным. Если полученное значение больше заданного, берут меньшее сечение и опять определяют
больше заданного, берут меньшее сечение и опять определяют ; если полученное значение
; если полученное значение меньше заданного – увеличивают сечение. Таким образом с помощью нескольких проб определяют нужные размеры сечения.
меньше заданного – увеличивают сечение. Таким образом с помощью нескольких проб определяют нужные размеры сечения.