Управление запасами
Для осуществления выпуска продукции необходимы определенные запасы материалов, комплектующих изделий, готовой продукции и т.д. Поддержание высокого уровни запасов является гарантией бесперебойной работы. С другой стороны, создание запасов требует дополнительных издержек на хранение, складирование, транспортировку, страхование и т.п. Модели управления запасами позволяют определить такой оптимальный уровень запаса, при котором минимизируются издержки на его создание и поддержание при заданном уровне непрерывности производственных процессов.
Наиболее простой моделью управления запасами является модель оптимального размера заказа (модель Уилсона). Модель основана на минимизации совокупных затрат по выполнению заказа и хранению запасов.
Затраты на выполнение заказа (транспортно-заготовительные расходы) – это накладные расходы, связанные с реализацией заказа и зависящие от размера заказа. Они могут быть рассчитаны как
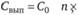
где С0 – транспортно-заготовительные расходы в расчете на один заказ (одну партию); п – количество заказов (партий) в год.
Затраты на хранение запаса представляют собой расходы на ОГЛАВЛЕНИЕ запаса на складе. Они рассчитываются по следующей формуле:
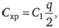
где 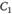 – затраты хранения единицы запаса; q – объем заказа (партии).
– затраты хранения единицы запаса; q – объем заказа (партии).
Выражение q/2 характеризует то, что затраты на хранение определяются средним уровнем запасов.
Общие затраты составят:
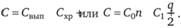
Таким образом, критерием оптимальности размера заказываемой партии является минимум общих затрат. Объем заказа (партии), при котором ,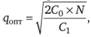 рассчитывается по формуле.
рассчитывается по формуле.
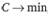
где N – годовая потребность в запасе.
Определив оптимальный размер заказа, можно определить оптимальное число поставок за год и продолжительность цикла изменения запаса.
Оптимальное количество заказов (партий):
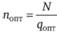
Оптимальный интервал между поставками:
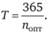
С учетом полученных значений минимальные совокупные затраты можно определить как

При определении оптимального размера заказа используются следующие допущения:
• известно общее число единиц запаса, составляющее годовую потребность;
• величина спроса постоянна;
• выполнение заказов происходит немедленно;
• расходы на оформление заказа не зависят от величины партии;
• цены на материалы не меняются в рассматриваемом периоде.
Пример
Ежегодный спрос предприятия на сырье для выпуска продукции составляет 18 000 единиц. Поставки осуществляются один раз в месяц. Транспортно-заготовительные расходы на доставку одной партии сырья составляют 2400 руб. Затраты на хранение единицы запаса – 60 руб./год. Определить оптимальный размер партии сырья и величину минимальных суммарных затрат.
Объем одного заказа (q) –1500 единиц (18000 :12).
Количество заказов в год (п) –12 (18000 :1500).
Суммарные затраты на доставку и хранение запасов:
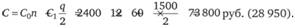
Оптимальный объем одного заказа:

Оптимальное количество заказов в год – 15 (18 000 : 1200).
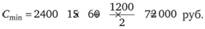
Экономия затрат после перехода на оптимальную партию заказа составит:
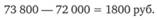
Вывод. Переход на оптимальную партию заказа экономически целесообразен.
Сетевые графики
Сетевой график – это экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией исследовательского или производственного проекта в их логической и технологической последовательности и связи.
Анализ сетевой модели, представленной в графической или табличной (матричной) форме, позволяет, во-первых, более четко выявить взаимосвязи этапов реализации проекта и, во-вторых, определить наиболее оптимальный порядок выполнения этих этапов в целях, например, сокращения сроков выполнения всего комплекса работ.
Основными элементами сетевого графика являются: работа, событие и путь.
Работа – это процесс, требующий затрат времени и ресурсов. На графике работа изображается стрелкой, которая соединяет два события. Работа выражается через (i,j)), где i – номер события, из которого работа выходит, a j – номер события, в которое она входит. Продолжительность выполнения работы обозначается как
Событие характеризует факт выполнения одной или нескольких работ. Событие не имеет продолжительности во времени. Событие имеет двойственный характер: для всех непосредственно предшествующих ему работ событие является конечным, а для всех непосредственно следующих за ним – начальным. Событиям присваивается порядковый номер (i = 1, 2, ..., N). Его желательно присваивать так, чтобы для любой работы номер конечного события был больше, чем номер начального события этой же работы. В сетевом графике события изображаются кружками.
Путь – это цепочка следующих друг за другом работ, соединяющих начальное и конечное события. Путь (L) обозначается в виде последовательности номеров событий. Путь, имеющий наибольшую продолжительность (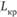 ), называется критическим. Критический путь определяет общую продолжительность работ (
), называется критическим. Критический путь определяет общую продолжительность работ (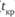 ). Все остальные пути имеют меньшую продолжительность, и поэтому в них выполняемые работы имеют резервы времени. Критический путь обозначается на сетевом графике утолщенными стрелками.
). Все остальные пути имеют меньшую продолжительность, и поэтому в них выполняемые работы имеют резервы времени. Критический путь обозначается на сетевом графике утолщенными стрелками.
Построение сетевых графиков подчиняется определенным требованиям:
1) в сетевом графике должно быть только одно начальное и конечное событие;
2) в сетевом графике не должно быть тупиков, т.е. событий, в которые входят работы, но из них не выходят (кроме конечного события);
3) в сетевом графике не должно быть событий, которым бы не предшествовала хотя бы одна работа (кроме начального события);
4) в сетевом графике не должно быть нескольких работ под одним и тем же номером;
5) в сетевом графике не должно быть циклов.
Важнейшими показателями сетевого графика являются
резервы времени. Поскольку каждый некритический путь сетевого графика имеет свой полный резерв времени, то и каждое событие этого пути имеет свой резерв времени.
Для определения резервов времени по событиям графика рассчитывают ранние и поздние сроки свершения событий.
Ранний срок 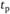 свершения события j определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события:
свершения события j определяется величиной наиболее длительного отрезка пути от исходного до рассматриваемого события:
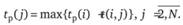
Поздний срок 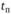 свершения события i характеризует самый поздний допустимый срок, к которому должно свершиться событие, не вызывая при этом срыва срока свершения конечного события:
свершения события i характеризует самый поздний допустимый срок, к которому должно свершиться событие, не вызывая при этом срыва срока свершения конечного события:
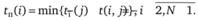
Все события, за исключением событий, принадлежащих критическому пути, имеют резерв времени R(i). Резерв показывает, на какой предельно допустимый срок может задержаться свершение события i без нарушения срока наступления завершающего события:
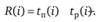
Для всех работ (i,j) на основе ранних и поздних сроков свершения событий можно определить следующие показатели.
Ранний срок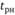 начала работы (i,j) совпадает с ранним сроком свершения события i:
начала работы (i,j) совпадает с ранним сроком свершения события i:
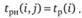
Ранний срок окончания работы 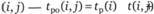 .
.
Поздний срок начала работы 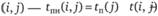 .
.
Поздний срок окончания работы 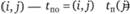 .
.
Полный резерв времени 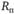 работы (i, j) показывает, насколько можно увеличить время выполнения данной работы при условии, что весь комплекс работ будет завершен в критический срок.
работы (i, j) показывает, насколько можно увеличить время выполнения данной работы при условии, что весь комплекс работ будет завершен в критический срок.
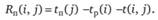
Работы, лежащие на критическом пути, резервов времени не имеют.
Частный резерв времени 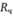 работы (i, j) – это часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки.
работы (i, j) – это часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки.
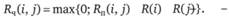
Пример
Необходимо провести маркетинговый анализ для обеспечения реализации нового продукта. Аналитик выделил работы для выполнения анализа и их продолжительность в днях.
|
Работа |
Предшествующие работы |
Продолжительность |
|
А. Формулирование проблемы |
1 |
|
|
В. Определение необходимой информации и источников ее получения |
А |
2 |
|
С. Выбор методики исследования |
А |
5 |
|
D. Согласование методики |
С |
3 |
|
Е. Изучение рыночной среды |
В |
4 |
|
F. Опрос респондентов |
С |
2 |
|
G. Обработка и анализ данных |
E, F |
7 |
|
Н. Подготовка отчета |
D, G |
2 |
На основе работ строится сетевой график исследования, который отражает последовательность выполнения работ.
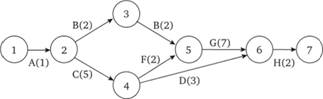
Выделим пути в сетевом графике:
• путь 1→2→3→5→6→7 (продолжительность 1 + 2 + 4 + + 7 + 2 = 16 дней);
• путь 1→2→4→5→6→7 (продолжительность 1 + 5 + 2 + + 7 + 2 = 17 дней);
• путь 1→2→4→6→7 (продолжительность 1 + 5 + 3 + 2 = = 11 дней).
Второй путь имеет наибольшую продолжительность в днях и является критическим. На графике он выделен утолщенными стрелками. Быстрее, чем за 17 дней, исследование выполнить нельзя, так как для достижения завершающего события критический путь должен быть пройден обязательно.
Проведем расчет параметров сетевого графика в таблице.
|
(i, j) |
t(i, j) |
tрн(i, j) = tp(i) |
tрo(i, j) |
tпн(i, j) |
tпо(i, j) = tп(i) |
Rп |
Rн |
Кп |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
(1,2) |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1,00 |
|
(2, 3) |
2 |
1 |
3 |
2 |
4 |
1 |
0 |
0,86 |
|
(2,4) |
5 |
1 |
6 |
1 |
6 |
0 |
0 |
1,00 |
|
(3, 5) |
4 |
3 |
7 |
4 |
8 |
1 |
1 |
0,86 |
|
(4, 5) |
2 |
6 |
8 |
6 |
8 |
0 |
0 |
1,00 |
|
(4,6) |
3 |
6 |
9 |
12 |
15 |
6 |
6 |
0,33 |
|
(5, 6) |
7 |
8 |
15 |
8 |
15 |
0 |
0 |
1,00 |
|
(6, 7) |
2 |
15 |
17 |
15 |
17 |
0 |
0 |
1,00 |
Показатели первой и второй графы показывают работы и их продолжительность.
Раннее время начала и окончания работ (графы 3 и 4) определяется прямым ходом, т.е. от начального события к конечному. Ранний срок начала работы, выходящей из события 1, принимается равным нулю, а ранний срок окончания – продолжительности этой работы. При этом время раннего начала последующих работ, выходящих из одного события, принимается по наибольшему значению времени позднего окончания предыдущей работы, входящей в это событие. Например, для работы (5, 6) ранний срок начала работы принимается из максимального времени раннего срока окончания работ (3, 5) и (4, 5), что соответствует значению 8, а для работы (6, 7) из сроков окончания работ (4, 6) и (5, 6), что соответствует значению 15.
Позднее начало и окончание работ (графы 5 и 6) определяются обратным ходом, т.е. от конечного события к начальному. Сначала определяется время позднего окончания работ, входящих в конечное событие, которое принимается равным наибольшему значению времени позднего окончания. В примере позднее окончание работы (6, 7) будет равно 17, что соответствует продолжительности критического пути. Позднее начало любой последующей работы определяется как разность ее позднего окончания и продолжительности самой работы. Позднее окончание предыдущих работ принимается равным наименьшему значению позднего начала последующих работ, выходящих из данного события.
Полный резерв времени (графа 7) определяется как разность граф 5 и 3 или 6 и 4.
Частный резерв времени (графа 8) определяется как разность между временем раннего окончания и раннего начала работы и продолжительности работы. В тех случаях, когда для ряда работ имеется несколько значений времени раннего окончания, в расчет принимается наибольшее время. Так, для работы (3,5) значение частного резерва будет получено выражением 8-3-4 = 1, а не 7-3-4 = 0, так как событие 5 произойдет только через восемь, а не через семь дней. Аналогично производим расчет для работы (4, 6) : 15 – б – -3 = 6 вместо 9-6-3 = 0.
Частные резервы времени характеризуют, что работу (3, 5) можно задержать на один день, что никак не отразится на выполнении маркетингового исследования в срок. В свою очередь, работа (4, 6) может задержаться на шесть дней, и это не отразится на времени начала последующей работы (6, 7) и сроке исследования в целом. Возможны и такие ситуации, при которых частный резерв времени выполнения одной из работ частично используется при выполнении данной работы, а частично передается другой работе. То есть часть резерва работы (4, 6) можно передать работе (3, 5).
Для оптимизации сетевых графиков оценивается степень напряженности выполнения всех работ. Для этого рассчитываются коэффициенты трудоемкости (графа 9) по следующей формуле:
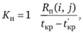
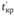 – общая продолжительность отрезков пути, проходящего через работу (i, j), совпадающих с критическим путем. Для работ критического пути коэффициенты напряженности равны 1. Для остальных работ:
– общая продолжительность отрезков пути, проходящего через работу (i, j), совпадающих с критическим путем. Для работ критического пути коэффициенты напряженности равны 1. Для остальных работ:

В классификации коэффициентов напряженности выделяют:
• напряженные – 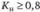 ;
;
• подкритические – 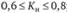 ;
;
• резервные – 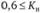
Рассчитанные значения коэффициентов показывают, что наряду с критическими работы (2, 3) и (3, 5) являются напряженными, а работу (4,6) можно отнести к резервной. Следовательно, оптимизация сетевого графика возможна только за счет резервной работы (4, 6). Это достигается уплотнением сетевого графика методом последовательных приближений, т.е. многократным сжатием очередного критического пути, пока не будет достигнут удовлетворительный результат.
Оптимизацию сетевого графика можно произвести с помощью линейного программирования. Предположим, что время критического пути в маркетинговом анализе необходимо уменьшить до 14 дней посредством форсирования критических работ. На сетевом графике выделены пять критических работ. Обозначим их как 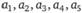 . Известно, что в работу необходимо вложить средства х,•, размером не более с,•, при этом время выполнения работы будет сокращаться согласно линейной зависимости:
. Известно, что в работу необходимо вложить средства х,•, размером не более с,•, при этом время выполнения работы будет сокращаться согласно линейной зависимости:
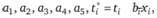
где 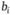 – некоторый положительный коэффициент линейной функции.
– некоторый положительный коэффициент линейной функции.
Предположим, что для критических работ коэффициенты равны:
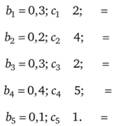
Требуется определить распределение 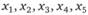 так, чтобы срок выполнения комплекса работ был не более 14 дней (
так, чтобы срок выполнения комплекса работ был не более 14 дней (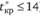 ), и сумма вложенных ресурсов была минимальной,
), и сумма вложенных ресурсов была минимальной,
например:
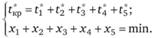
Запишем выражение для нового значения критического пути:
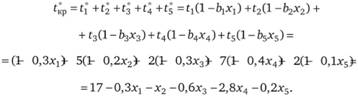
С учетом нового срока исследования
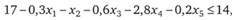
или 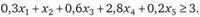
Задача линейного программирования может быть сформулирована следующим образом.
Определить минимум целевой функции 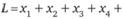
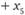 при условиях:
при условиях:
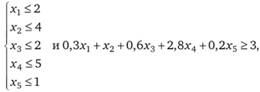
при неотрицательных переменных 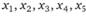 .
.