Цена облигации и процентная ставка

Для определения связи между ценой облигаций и ставкой процента воспользуемся методом дисконтирования. В экономической науке он применяется для приведения величины будущих доходов к сегодняшней стоимости, например, когда надо определить, сколько средств необходимо вложить сегодня (при данной ставке процента), чтобы получить некоторую сумму в будущем.

Рассмотрим процесс дисконтирования на простом примере с дисконтной облигацией.

Дисконтная облигация - это облигация, которая покупается по цене (Рb - bond price, цена облигации) ниже номинала (со скидкой), а ее номинальная стоимость выплачивается в момент погашения облигации. Например, дисконтная облигация номиналом 1000 руб. продается сегодня за 909 руб., а через год ее владелец получит 1000 руб. Тогда процентный доход будет равен 10%. Чтобы в текущий момент сравнивать ожидаемую доходность различных активов, необходимо рассмотреть понятие текущей стоимости будущих доходов (PV - present value, текущая стоимость будущих доходов). Текущая стоимость показывает, сколько средств необходимо вложить сегодня (при заданной ставке процента), чтобы получить в будущем определенную сумму. В нашем случае сегодня необходимо вложить 909 руб., чтобы через год (при ставке 10%) получить 1000 руб.:

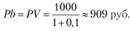
Попробуем определить текущую стоимость PV облигации со сроком погашения два года:

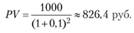
Понятно, что чем дальше в будущее отодвинут срок погашения долга, тем на большую величину будет дисконтирована сумма. Пусть ежегодный фиксированный доход по облигации равен A. Тогда текущая стоимость всего потока будущих доходов r за n лет, дисконтированная по ставке процента, будет

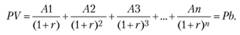
Для простоты предположим, что облигация гарантирует выплату определенной фиксированной суммы А бесконечно, тогда А1 = А2 = =АЗ =... = Ап. Такая облигация носит название консоли. Текущая стоимость консоли представляет дисконтированную величину платежей по ней:

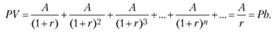
Отсюда видно, что цена консоли находится в обратной зависимости от процентной ставки. Для облигаций с конечным сроком погашения эта зависимость будет более сложной. По общий вывод остается тем же: более высокая ставка процента предполагает более низкие цены на облигации.

Таким образом, цена облигации и ставка процента находятся в обратной зависимости: чем выше процентный доход, тем меньше надо заплатить сейчас, чтобы получить определенную сумму дохода в будущем, т.е. с ростом процентной ставки цепа облигаций падает, соответственно, спрос на них растет, так как экономические агенты предпочитают покупать облигации, а не оставлять на руках деньги. Это означает, что спрос на деньги при высокой ставке процента будет небольшим.

Домохозяйства, принимая портфельное решение об объеме вложений в ценные бумаги, одновременно формируют величину спекулятивного спроса на деньги. Так как люди стремятся получить максимальный доход от своих вложений, то величина спроса на ценные бумаги находится в прямой зависимости от их доходности (номинальной ставки процента). Повышение процентной ставки приводит к увеличению альтернативных издержек хранения денег и, следовательно, к снижению величины спроса на деньги. Можно заключить, что население будет менять объем спроса на ценные бумаги и денежные средства в зависимости от величины номинальной ставки процента. Отсюда следует, что спекулятивный спрос на деньги можно представить в виде функции, аргументом которой является номинальная ставка процента.

Следует обратить внимание, что номинальная ставка процента зависит от реальной ставки процента и ожидаемого темпа инфляции π^е, который, в свою очередь, зависит от роста денежной массы.

ВОПРОСЫ ТЕОРИИ