Теоремы теории подобия. Критерии подобия

Очевидно, что подобные явления должны принадлежать лишь к одному классу, т.е. описываться одной и той же системой дифференциальных уравнений. В общем случае дифференциальные уравнения не могут удовлетворяться одновременно при переменных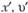и т.д. и при новых переменных 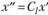', 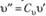и т.д. Таким образом, в общем случае дифференциальные уравнения и уравнения группового преобразования несовместны.

Покажем, что, для того чтобы переменные одновременно удовлетворяли дифференциальным уравнениям и уравнениям группового преобразования, множители 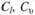и т.д. не могут выбираться произвольно, а связаны определенными соотношениями.

Выпишем одно из уравнений Навье – Стокса для 1-го явления (образца):

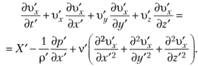(5.4)

Для 2-го явления (модели), подобного 1-му, положим

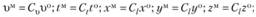
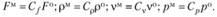(5.5)

Уравнение Навье – Стокса для модели будет

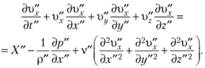(5.6)

Подставляя соотношения (5.5) в уравнение (5.6) и учитывая, что константы подобия постоянны и при дифференцировании выносятся за знак дифференциала, получаем

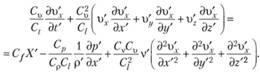(5.7)

Из соотношения (5.7) можно заключить, что для совместности уравнений (5.4) и (5.6), т.е. для того чтобы переменные 1-го и 2-го явлений удовлетворяли бы одному и тому же дифференциальному уравнению, должно быть выполнено

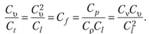
Или, разделив все па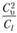, найдем

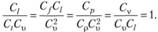
Отсюда

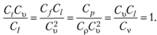
Учитывая, что из соотношений (5.5) 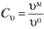и т.д., получаем

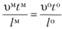, или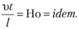

Таким образом, комплекс величин (чисел подобия) в соответствующих точках образца и модели должен быть неизменен (условие равенства чисел подобия обозначается значком idem):

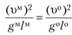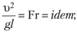
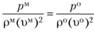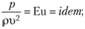
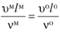, или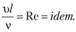

Величины Но, Fr, Eu, Re называют критериями подобия (числами подобия): Но – критерий гомохронности; Fr – критерий Фруда; Eu – критерий Эйлера; Re – критерий Рейнольдса. Отметим, что кроме перечисленных, могут быть и другие критерии подобия (см. параграф 5.3).

Первая теорема подобия (теорема Ньютона) при этом формулируется следующим образом: у подобных явлений для любой пары соответственных точек критерии подобия численно одинаковы. При переходе от одной пары соответственных точек к другой критерии подобия изменяют значение. Эта теорема дает необходимые условия подобия.

Рассмотрим теперь условия, которые достаточны для того, чтобы явления в модели и образце были подобны. Понятие подобия распространяется на все соответственные точки подобных систем, в том числе на границах систем, а также в начальный момент времени. Но отдельные явления различаются между собой лишь условиями однозначности. Поэтому если условия однозначности сделать подобными, то и сами явления окажутся подобными, если они описываются одними и теми же дифференциальными уравнениями. Но для подобия условий однозначности достаточно соблюсти равенство критериев подобия, составленных лишь из величин, входящих в условия однозначности. Поэтому можно сказать: подобны те явления, условия однозначности которых подобны, а критерии подобия, составленные из величину входящих в условия однозначности, равны. Это утверждение составляет третью теорему подобия (теорему Кирпичева – Гухмана).

Значение этой теоремы состоит в том, что она позволяет воспроизводить подобные явления, т.е. моделировать их. Согласно этой теореме, для того чтобы модель была подобна образцу, достаточно обеспечить пропорциональность всех величин на границе явления и в начальный момент времени, выбрав эти величины так, чтобы критерии, составленные из них, были численно равны для соответствующих точек модели и образца.

Например, при течении жидкости в гладкой круглой трубе в условия однозначности входят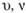. Поэтому должно быть 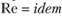, или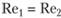. Отсюда ^[1]

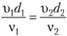
Есл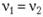и и 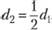, то на входе должно быть 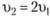. Именно в этом случае условия однозначности будут подобны.

Все критерии, полученные из данной системы уравнений, можно разбить на две категории. К первой категории относятся критерии, составленные из величин, входящих в условия однозначности. Эти критерии называются определяющими, так как они определяют достаточные условия подобия. Ко второй относятся все остальные критерии, получающиеся из системы уравнений. Они называются неопределяющими.

Если значения определяющих критериев у двух явлений в соответственных точках равны, то явления подобны. Но если они подобны, то по первой теореме подобия они имеют в соответственных точках одинаковые значения всех критериев, независимо от того, к какой из двух категорий они относятся. Отсюда следует, что равенство определяющих критериев имеет следствием равенство всех остальных критериев. А это означает существование функциональной зависимости между определяющими и неопределяющими критериями.

В самом деле, если мы перейдем от одних значений определяющих критериев к другим, то мы перейдем от одной группы подобных явлений к другой. Но при этом и все остальные неопределяющие критерии получат какие-то новые единственные значения. Таким образом, каждый неопределяющий критерий есть однозначная функция определяющих критериев. Например,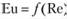i.

Вид этой функции может быть найден из опыта. Если мы получим из опыта зависимость 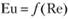и построим эту зависимость в виде графика, то каждая точка на таком графике будет отвечать целой группе подобных явлений, для которых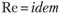, а вся кривая в целом – серии групп.

Между тем одна точка на графике может быть получена в результате единичного опыта, а вся кривая – в виде небольшой серии опытов на единственной установке. Например, после того как найдено число 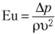, перепад давлений 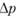находится по формуле .

Таким образом, мы можем обобщить результаты единичного эксперимента на целую серию групп и получить решение или интеграл дифференциального уравнения в виде критериального уравнения. Отсюда следует вторая теорема подобия (теорема Федермана – Букингема), которая формулируется следующим образом: решение системы дифференциальных уравнений может быть представлено в виде функции между критериями подобия этой системы.

Значение второй теоремы подобия состоит в том, что она позволяет не интегрировать систему дифференциальных уравнений, а получать ее интеграл из опыта в виде критериального уравнения. Кроме того, она указывает на то, что данные опыта должны обрабатываться в виде функциональной зависимости между критериями подобия.