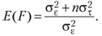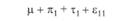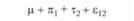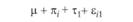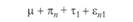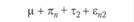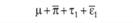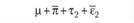Структурная модель

Структурная модель однофакторного дисперсионного анализа с повторными измерениями так же, как и известная нам модель обычного дисперсионного анализа, относится к общим линейным моделям. Она предполагает по меньшей мере четыре аддитивных составляющих зависимой переменной:

• популяционную постоянную μ;

• эффект независимой переменной τj, специфичный и постоянный для каждого ее уровня;

• индивидуальную константу πi, выражающую эффект отдельного испытуемого (предполагается, что ее значение в генеральной совокупности равно 0);

• неконтролируемую экспериментальную ошибку ij.

Строго говоря, нет оснований предполагать, что эффекты независимой переменной и испытуемого действительно оказываются несвязанными друг с другом. Поэтому к этим четырем составляющим необходимо добавить совокупный эффект πi и τj, выражающий их взаимодействие^[1] – 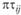. Поскольку этот эффект в рассматриваемом экспериментальном плане выделить нельзя, нет необходимости его рассматривать. Будем исходить из того, что результат, получаемый в эксперименте, воплощающем однофакторный план с повторным измерением, описывается следующим соотношением:

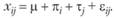
Необходимо также предположить нормальность распределения полученных в эксперименте данных. Учитывая приведенное базовое соотношение исследуемых параметров, это будет означать справедливость следующих допущений.

• Экспериментальная ошибка представляет собой случайную величину, распределенную в соответствии с нормальным законом с математическим ожиданием, равным нулю.

• Индивидуальная константа представляет собой также случайную величину, распределенную в популяции рассматриваемых данных в соответствии с нормальным законом, при этом ее математическое ожидание также равно нулю.

• Эффект экспериментального воздействия представляет собой случайную величину, распределенную в соответствии с нормальным законом с заранее неизвестными параметрами.

Пользуясь этими базовыми предпосылками, можно построить модель, описывающую структуру полученных в эксперименте данных. Легче будет начать с обсуждения более простого и, возможно, более распространенного случая, когда число уровней независимой переменной ограничено двумя. В этом случае выдвинутые исходные предположения оказываются исчерпывающими.

Таблица 4.3

Структурная модель однофакторною дисперсионною анализа с повторным измерением для двухуровневой переменной

Испытуемые	Уровень 1 (T1)	Уровень 2 (Τ2)
1
…	…	…
i
…	…	…
n
Среднее

Таблица 4.3 резюмирует логику структурной модели однофакторного экспериментального плана с повторным измерением для двухуровневых переменных. Мы видим, что, поскольку величины μ, τ1 и τ2 постоянны, дисперсия внутри каждого экспериментального условия определяется дисперсией экспериментальной ошибки σ2 и дисперсией индивидуального эффекта .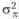

Поскольку экспериментальная ошибка ε происходит из одного и того же источника, логично считать, что

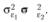
Таким образом, будут справедливы следующие соотношения:

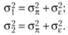
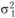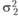Здесь и – дисперсия данных внутри первого и второго экспериментального условия соответственно. Величины 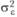в приведенных уравнениях являются статистически независимыми друг от друга, чего нельзя сказать о величинах 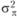. По сути, величина 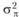является общей для двух экспериментальных условий. Таким образом, она определяет статистическую связь двух экспериментальных условий – Т1 и Т2). Иными словами, эффект испытуемого представляет собой ковариацию двух экспериментальных условий Т1 и Т2 – σ12.

Следовательно, ожидаемая величина остаточной дисперсии, т.е. дисперсии экспериментальной ошибки, должна определяться следующим соотношением:

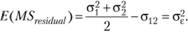
Нетрудно также показать, что ожидаемая величина статистики MSlreatment будет определяться таким образом:

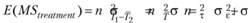
Отсюда, ожидаемая величина статистики F будет равна

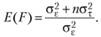
Теперь можно выдвинуть нулевую статистическую гипотезу о равенстве эффектов независимой переменной τ. Это означает, что дисперсия эффектов независимой переменной – 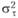– оказывается равной нулю. Тогда очевидно ожидаемое значение статистики доказывается равным единице. В противном случае, когда эффекты независимой переменной различаются на двух уровнях, ожидаемое значение статистики /'должно превышать единицу.

Таким образом, если верны первоначальные предположения структурной модели для двухуровневого экспериментального плана с повторными измерениями, то вычисленная статистика F должна вести себя в соответствии с F-распределением, характеризующимся одной степенью свободы в числителе и n – 1 степенями свободы в знаменателе. В таком случае проверка выдвинутой гипотезы осуществляется известным нам способом, т.е. в результате оценки вероятности получить значение F, равное (или даже большее) наблюдаемому. Заметим, что, как и в случае межгруппового дисперсионного анализа, теоретически невозможно получить значение F, меньшее единицы, поэтому если такой результат будет получен на практике, это будет означать безусловное принятие нулевой гипотезы.

Несколько сложнее обстоит дело в случае, когда экспериментатор решил использовать более двух уровней независимой переменной.

Пусть в эксперименте приняли участие п испытуемых и было использовано k уровней независимой переменной. Тогда в соответствии с базовой моделью однофакторного экспериментального плана с повторными измерениями дисперсия данных на произвольном уровне j независимой переменной будет определяться следующим образом:

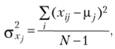
где μj – популяционная средняя для у-го уровня независимой переменной – μ + τ,j; N – число испытуемых в генеральной совокупности.

Величина μ, теоретически может быть рассчитана но формуле

Ковариация данных между двумя произвольно выбранными уровнями независимой переменной может быть оценена следующим образом:

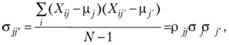
где r – величина корреляции между Хj и Хj.

Величины ковариаций для всех пар уровней формируют так называемую ковариационно-вариационную матрицу Ckk, диагональ которой образуют значения 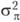. Заметим, что матрица ковариаций оказывается симметричной относительно диагонали 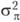. Так, если величина k (число уровней независимой переменной) оказывается равной четырем, ковариационно-вариационная матрица С44 будет иметь следующий вид:

Иными словами, предполагается, что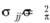

Это предположение получило название гипотезы о гомогенности вариационно-ковариационной матрицы. Такая гомогенность представляет собой проявление составной симметрии, которая, в свою очередь, отражает эффект сферичности. Матрица экспериментальных результатов Хnk, которую еще иногда называют матрицей смешения, будет считаться сферичной, если дисперсии

всех разностей экспериментальных условий , получаются одинаковыми.

Если такое допущение оказывается действительно верным, тогда дисперсия зависимой переменной на каждом уровне независимой переменной определяется лишь двумя факторами – фактором экспериментальной ошибки и фактором испытуемого, который целиком определяет ковариации данных:

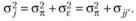(4.5)

Отсюда дисперсия экспериментальной ошибки (остаточная дисперсия) будет описываться следующим соотношением:

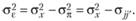
Дисперсию данных внутри одного экспериментального условия оценить несложно. Пусть

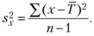
Тогда при выполнении исходных требований структурной модели должно быть справедливо следующее соотношение:

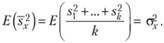
Величину остаточной дисперсии, связанной с экспериментальной ошибкой, можно теперь оценить, используя соотношение (4.5), т.е. вычитая среднюю величину ковариации из среднего значения дисперсии внутри экспериментальных условий, т.е.

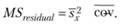(4.6)

Формула (4.6) эквивалентна известной нам формуле для вычисления величины остаточной дисперсии (4.3), хотя и требует больших вычислительных усилий. Таким образом, ожидаемое значение остаточной дисперсии, вычисленной по формуле (4.6), должно описываться следующим соотношением:

Если все допущения структурной модели, включая особенно важное допущение об однородности вариационно-ковариационной матрицы, выполняются, то статистика 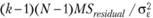будет описываться распределением 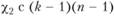степенями свободы.

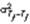
Дисперсия, вызванная эффектом экспериментального воздействия MStreatment, оценивается стандартным образом. Ожидаемое значение для этой статистики описывается следующим соотношением:

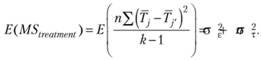
Статистика MStreatment также описывается распределением χ2, но с k – 1 степенью свободы.

Таким образом, мы приходим к уже известному нам соотношению, описывающему ожидаемое значение F-статистики: