Средние показатели в рядах динамики и методы их исчисления
Каждый ряд динамики можно рассматривать как некую совокупность т меняющихся во времени показателей, обобщенных в виде средних величин. Для обобщения данных но рядам динамики рассчитывают средний уровень ряда динамики, средний абсолютный прирост, средние темпы роста и прироста.
Средний уровень ряда динамики (у) рассчитывается по средней хронологической. Средней хронологической называется средняя, исчисленная из значений, изменяющихся во времени. Такие средние обобщают хронологическую вариацию. В хронологической средней отражается совокупность тех условий, в которых развивалось изучаемое явление в данном промежутке времени.
Средний уровень ряда определяется по-разному для моментных и интервальных рядов.
Для интервальных равноотстоящих рядов средней уровень находят по формуле простой средней арифметической:

где и — число уровней или длина ряда.
Для интервальных неравностоящих рядов средний уровень вычисляют по формуле взвешенной средней арифметической:
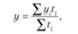
где tj — продолжительность интервалов времени между уровнями (число периодов времени, при которых значение уровня не изменяется).
Пример. Интервальный ряд динамики с равноотстоящими уровнями приведен в табл. 8.5. По этим данным можно рассчитать среднегодовой уровень числа проданных квартир за 2006—2010 гг. Он будет равен 109,6 тыс. ед. (у = 548/5), т.е. в среднем ежегодно число проданных квартир в регионе за 2006—2010 гг. составило полученное значение.
Средний уровень моментного равноотстоящего ряда динамики определяют по формуле средней хронологической простой:

Средний уровень моментных рядов динамики с неравно-отстоящими уровнями определяется по формуле средней хронологической взвешенной:

где Ь1 — продолжительность интервала времени между соседними уровнями, г = 1, 2,п.
Пример. Покажем расчет среднего уровня моментного ряда динамики с равноотстоящими уровнями по данным о численности работников строительной фирмы на 1-е число каждого месяца 2010 г. (человек):
1 января...........................................347
1 февраля.........................................350
1 марта..............................................349
1 апреля............................................351
Среднемесячная численность работников фирмы за I квартал (см. формулу (8.11)) составит

Пример. Известна списочная численность рабочих промышленной организации на некоторые даты (человек). Ряд динамики имеет неравноотстоящие уровни во времени:
1 января 2010 г................................530
1 марта 2010 г...................................570
1 июня 2010 і-...................................520
1 сентября 2010 г............................430
1 января 2011 г................................550
Среднегодовая численность работников за 2010 г. (см. формулу (8.12)) составит:
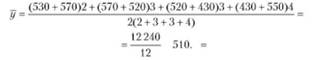
Средний абсолютный прирост за весь период, ограничивающий ряд динамики, — это обобщающий показатель абсолютной скорости изменения явления во времени. Скоростью в данном случае будем называть прирост (уменьшение) в единицу времени. Для его определения используют формулу простой средней арифметической:

Подставив в числитель выражение для цепных абсолютных приростов, получим более удобную форму записи для среднего абсолютного прироста:

где уп, у{ — конечный и начальный уровни ряда динамики соответственно.
Пример. По данным табл. 8.5 определим средний абсолютный прирост числа проданных квартир за период 2006—2010 гг. Он составит (112 - 108)/4 = 1,0 тыс. ед.
Средний темп роста служит сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики. Он показывает, сколько в среднем процентов последующий уровень составляет от предыдущего в течение всего периода наблюдения.
Средний темп (коэффициент) роста рассчитывают но формуле средней геометрической из цепных коэффициентов роста:

где К1 — цепные коэффициенты роста.
Выразив цепные коэффициенты (темпы) роста через соответствующие уровни ряда, получим:

Пример. По данным табл. 8.5 рассчитаем средний темп роста числа проданных квартир за период 2006—2010 гг. (см. формулу (8.13))

или по формуле

Когда приходится производить расчет средних темпов роста по периодам различной продолжительности (неравноотстоящие уровни), используют среднюю геометрическую, взвешенную по продолжительности периодов. Формула средней геометрической взвешенной будет иметь следующий вид:

где I — интервал времени, в течение которого сохраняется данный темп роста.
Средний темп прироста не может быть определен непосредственно на основании последовательных темпов прироста. Для его вычисления необходимо сначала найти средний темп роста, а затем уменьшить его на единицу или на 100%:

Пример. По данным табл. 8.5 был рассчитан средний темп роста числа проданных квартир за 2006—2010 гг., равный 100,9%, отсюда найдем средний темп прироста, %:
