Соответствие модели и проблема оценки сферичности

Рассмотренная нами структурная модель однофакторного дисперсионного анализа с повторными измерениями, как уже указывалось, базируется на двух принципиальных допущениях.

Первое допущение стандартно. Оно касается характера распределения исследуемой зависимой переменной X в генеральной совокупности. Так же, как и в случае обычного варианта дисперсионного анализа, используемого для сравнения нескольких экспериментальных групп, предполагается, что зависимая переменная распределена в соответствии с законом нормального распределения. Обычно это допущение не предполагает серьезных предварительных тестов, так как даже значительное отклонение в распределении зависимой переменной от нормального закона не ведет к серьезным отклонениям в распределении строящейся в ходе дисперсионного анализа Т-статистики, которая, как предполагается, должна описываться законом F-распределения. Однако этого нельзя сказать о втором допущении структурной модели ANOVA с повторными измерениями. Это допущение касается вариационно-ковариационной матрицы, и оно представляется весьма существенным.

Как мы помним, предполагается однородность, гомогенность, этой матрицы. Эта однородность касается как величин дисперсий зависимой переменной на всех ее уровнях, так и всех величин попарных ковариаций:

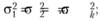
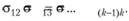
Предположение об однородности вариационно-ковариационной матрицы является очень существенным. Чем менее однородна вариационно-ковариационная матрица, тем менее распределение наблюдаемой статистики сходно с F-распределением, причем эти отклонения могут быть весьма большими даже при незначительной гетерогенности этой матрицы. В результате возникает опасность переоценить статистическую значимость вычисленного значения F.

Предположение структурной модели, касающееся однородности вариационно-ковариационной матрицы, значительно более важно, чем предположение о нормальности распределения исходных параметров. Поэтому оно требует специальных предварительных тестов, от которых может зависеть возможность использования стандартных процедур дисперсионного анализа. Обычно для оценки однородности вариационно-ковариационной матрицы используют широко распространенный и достаточно надежный тест сферичности Моучли (Mauchly). Возможность применения этого теста существует во всех более или менее распространенных статистических пакетах компьютерной обработки данных, таких как, например, пакет IBM SPSS Statistics. Если тест сферичности даст статистически надежный результат, это свидетельствует о необходимости отвергнуть гипотезу о сферичности дисперсии, и следовательно, о значительной неоднородности, гетерогенности, вариационно-ковариационной матрицы. Следует, однако, иметь в виду, что этот тест чувствителен к нормальности распределения данных. Поэтому в условиях, когда распределение исследуемой зависимой переменной отличается от нормального, тест Моучли может давать статистически надежный результат даже тогда, когда сферичность действительно имеет место.

Существует три основных способа разрешения проблемы гетерогенности вариационно-ковариационной матрицы (Mvers, Well, 2003. Р. 163; [291):

• изменение числа степеней свободы для числителя и знаменателя при использовании стандартного F-теста;

• использование мультивариативного теста MANOVA;

• применение тестов априорных контрастов.

Поправка на несферичность

Коррекция числа степеней свободы – это, пожалуй, наиболее распространенная процедура в ситуации неоднородности вариационно-ковариационной матрицы. В общем случае рекомендуется умножить соответствующие значения степеней свободы на некоторую величину q, находящуюся в диапазоне от 1 (полностью гомогенная матрица) до 1/(k – 1) (наименее гомогенная, гетерогенная матрица). Конкретное значение q определяется как функция гетерогенности исследуемой матрицы.

Такое уменьшение обеспечивает более высокую степень консервативности при принятии решения о статистических эффектах независимой переменной и, как следствие, уменьшение вероятности ошибки первого рода. Понятно, что наибольшая степень консервативности при принятии статистического решения обеспечивается при умножении числителя и знаменателя на величину 1/(/k – 1). В ряде случаев такая степень консервативности может оказаться избыточной, и тогда исследователь может недооценить имеющиеся между уровнями независимой переменной различия и, таким образом, допустить ошибку второго рода.

Поэтому в математической статистике разработаны более тонкие критерии оценки степеней свободы в случае гетерогенности вариационно-ковариационной матрицы. Они вносят некоторые поправки в структуру исследуемых данных, изменяя число степеней свободы с помощью параметра Θ. Наиболее известными и распространенными методами изменения числа степеней свободы являются алгоритмы Гринхауса – Гейсера и Хюнха – Фельдта, результат применения которых – поправка ε, представляющая в обоих случаях несмещенную оценку величины . Поскольку эти алгоритмы предлагают несколько отличные друг от друга способы оценки , величины ε, рассчитанные по этим двум алгоритмам, могут несколько различаться. Если применение этих поправок позволяет сделать противоположные выводы о необходимости принятия или отвержения нулевой гипотезы, рекомендуется отдать предпочтение поправке Гринхауса – Гейсера как более консервативной.