Собственно-случайная (простая случайная) выборка
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности в целом, без разделения ее на группы, подгруппы или серии отдельных единиц. При этом единицы отбираются в случайном порядке, не зависящем ни от последовательности расположения единиц в совокупности, ни от значений их признаков.
Прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений. Например, при обследовании торговых предприятий необходимо указать, включит ли в себя генеральная совокупность торговые павильоны, коммерческие палатки, передвижные торговые точки и прочие подобные объекты; при обследовании студентов важно определиться, будут ли приниматься во внимание студенты-заочники, экстерны, учащиеся в магистратуре, лица, находящиеся в академическом отпуске, и т.п.
Для проведения отбора единиц в выборочную совокупность используется один из математических алгоритмов, например, метод прямой реализации, включающий в себя следующие этапы.
1. Все единицы генеральной совокупности, расположенные в случайном порядке или ранжированные по какому-либо признаку, нумеруются от 1 до N.
2. С помощью процессора случайных чисел получают п значений в интервале от 1 до N. Если первоначально случайные числа получены в интервале от 0 до 1, их необходимо умножить на N и округлить по правилам до целого значения.
3. Из сформированного списка единиц генеральной совокупности отбираются единицы, соответствующие по номеру полученным случайным числам.
Упрощенным вариантом метода прямой реализации является отбор единиц в выборочную совокупность па основе таблицы случайных чисел (прил. 3). Для проведения отбора могут быть использованы цифры любого столбца данной таблицы, при этом необходимо учитывать объем генеральной совокупности.
Рассмотрим процедуру отбора на основе фрагмента таблицы случайных чисел. Предположим, объем генеральной совокупности составляет 70 000 ед. и требуется сформировать выборку объемом 500 ед. Цифры таблицы случайных чисел, приведенных в прил. 3, следует перегруппировать для получения пятизначных чисел следующим образом:
54 895 58 331 56 083 51 988
35 220 93 578 77 566 57 020
75 557 57 925 50 248 79 477
57 593 55 450 80 907 47 001
63 036 89 533 71319 67 231
Для формирования выборки нужно взять 500 чисел в интервале от 00001 до 70 000. Таким образом, из списка единиц генеральной совокупности следует отобрать единицы под номером 54 895, 35 220, 57 593 и т.д. При этом номера свыше 70 000 (75 557, 93 578 и подобные) будут проигнорированы.
При проведении бесповторного отбора повторяющиеся номера следует учитывать только один раз. При повторном отборе, если тот или иной номер случайно встретится еще один или более раз, соответствующая этому номеру единица в каждом случае повторно включается в выборочную совокупность.
После проведения отбора с использованием какого-либо алгоритма, реализующего принцип случайности, или на основе таблицы случайных чисел, необходимо определить границы генеральных характеристик. Для этого рассчитываются средняя и предельная ошибки выборки.
Средняя ошибка повторной собственно-случайной выборки определяется по формуле
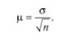
С учетом выбранного уровня вероятности и соответствующего ему значения £ предельная ошибка повторной собственно-случайной выборки составит:

Тогда можно утверждать, что при заданной вероятности генеральная средняя будет находиться в следующих границах:
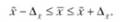
Предположим, в результате выборочного обследования доходов домохозяйств региона, осуществленного на основе собственно-случайной повторной выборки, получен следующий ряд распределения:
Доход, тыс. руб/чел.....До 5 5-10 10-15 15-20 20 и более
Число домохозяйств .....52 354 475 170 49
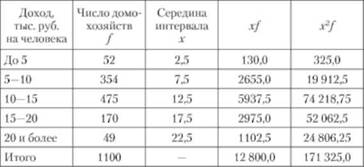
Рассмотрим определение границ генеральной средней, в данном примере — среднего дохода домохозяйства в целом по данному региону, опираясь только на результаты выборочного обследования. Для вычисления средней ошибки выборки необходимо прежде всего рассчитать выборочную среднюю величину и дисперсию изучаемого признака (табл. 10.1).
Таблица 10.1. Расчет среднего дохода домохозяйства и дисперсии
Таким образом,
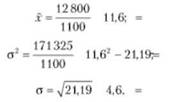
Средняя ошибка выборки составит:
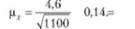
Определим предельную ошибку выборки с вероятностью 0,954 (¿ = 2):
Д. =2 0,14 =0,28. Установим границы генеральной средней, тыс. руб.: 11,6-0,28 <х< 11,6 + 0,28,
или
11,32<х< 11,88.
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,954 можно заключить, что средний доход домохозяйства в расчете на одного человека в целом но региону лежит в пределах от 11,3 тыс. до 11,9 тыс. руб.
При расчете средней ошибки собственно-случайной бесповторной выборки необходимо учитывать поправку на бесповторность отбора:

Если предположить, что представленные в ряде распределения данные являются результатом 5%-го бесповторного отбора (следовательно, генеральная совокупность включает в себя 22 000 домохозяйств), то средняя ошибка выборки будет несколько меньше:

Соответственно уменьшится и предельная ошибка выборки, что вызовет сужение границ генеральной средней. Особенно ощутимо влияние поправки на бесповторность отбора при относительно большом проценте выборки.
Мы рассмотрели определение границ генеральной средней. Рассмотрим теперь, как определяются границы генеральной доли, т.е. границы доли единиц, обладающих тем или иным значением признака.
Воспользуемся еще раз данными ряда распределения для того, чтобы определить границы доли домохозяйств, доходы которых составляют менее 10 тыс. руб. на одного человека. Согласно результатам обследования, численность таких домохозяйств составила 52 + 354 = 406. Определим выборочную долю и дисперсию:

Рассчитаем среднюю ошибку выборки:

Предельная ошибка выборки с ладанной вероятностью составит
Д., = 2-0,014 =0,028. Определим границы генеральной доли:
0,369 - 0,028 <р< 0,369 + 0,028,
или
0,341 <р< 0,397.
Следовательно, с вероятностью 0,954 можно утверждать, что доля домохозяйств, имеющих доходы менее 10 тыс. руб. на одного человека, в целом поданному региону находится в пределах от 34,1 до 39,7%.
Мы рассмотрели определение границ генеральной средней и генеральной доли по результатам уже проведенного выборочного наблюдения, при известном объеме выборки или проценте отбора. На этапе же проектирования выборочного наблюдения именно объем выборочной совокупности и требует определения.
Чем больше объем выборки, тем меньше значения средней и предельной ошибок выборочного наблюдения и, следовательно, тем уже границы генеральной средней и генеральной доли. В то же время необходимо учитывать, что большой объем выборки, как уже отмечалось выше, приводит к удорожанию обследования, увеличению сроков сбора и обработки материалов, требует привлечения дополнительного персонала и соответствующего материально-технического обеспечения. Затраты всех ресурсов на 20—30%-е выборочное наблюдение уже сопоставимы с расходами на сплошное обследование. При этом не следует забывать, что статистические характеристики, полученные по выборочной совокупности, всегда имеют вероятностную основу и будут уступать результатам сплошного наблюдения по точности и надежности. Поэтому при подготовке выборочного наблюдения необходимо определить тот минимально необходимый объем выборки, который обеспечит требуемую точность полученных статистических характеристик при заданном уровне вероятности.
Представим формулу (10.1) следующим образом:
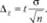
Отсюда можно вывести формулу для определения необходимого объема собственно-случайной повторной выборки:

Полученный на основе использования данной формулы результат всегда округляется в большую сторону. Например, если определено, что необходимый объем выборки составляет 493,1 ед., то, обследовав 493 ед., мы не достигнем требуемой точности. Поэтому для достижения желаемого результата обследованием должны быть охвачены 494 ед. Вместе с тем рассчитанное значение необходимого объема выборки свободно может быть увеличено в большую сторону на несколько единиц. Если мы располагаем необходимыми ресурсами, то по причинам организационного порядка (компактность расположения единиц, фиксированная нагрузка на каждого регистратора и т.п.) вполне можем охватить больший объем, и включение в выборочную совокупность 500 или, например, 550 ед. только уменьшит значения полученных случайной и предельной ошибок.
Как очевидно из формулы (10.3), необходимый объем выборки будет тем больше, чем выше заданный уровень вероятности и чем сильнее варьирует наблюдаемый признак. В то же время повышение допустимой предельной ошибки выборки приводит к снижению необходимого ее объема.
Расчет необходимого объема выборки предусматривает, что организаторы выборочного наблюдения уже на этапе его проектирования располагают по крайней мере косвенными данными о вариации изучаемых признаков. Источниками таких данных могут служить:
а) результаты исследования данного объекта в предшествующие периоды;
б) результаты исследования аналогичных объектов (жителей других населенных пунктов, предприятий других регионов и т.п.);
в) специально проведенное небольшое по объему выборочное обследование данного объекта, ставящее целью лишь изучение вариации наблюдаемых признаков.
При определении необходимого объема выборки для определения границ генеральной доли задача оценки вариации решается значительно проще. Если дисперсия изучаемого альтернативного признака неизвестна, то можно использовать ее максимальное возможное значение:

Например, предприятию связи с вероятностью 0,954 необходимо определить удельный вес телефонных разговоров продолжительностью менее 1 мин с предельной ошибкой 2%. Сколько разговоров нужно обследовать в порядке собственно-случайного повторного отбора для решения этой задачи?
Для получения ответа на поставленный вопрос воспользуемся формулой (10.3) и будем ориентироваться на максимальную возможную дисперсию доли телефонных разговоров такой продолжительности. Расчет приводит к следующему результату:
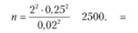
Таким образом, обследованием должны быть охвачены не менее 2500 разговоров па предмет их продолжительности.
Необходимый объем собственно-случайной бесповторной выборки может быть определен по следующей формуле:

Укажем на одну особенность формулы (10.4). При проведении вычислений объем генеральной совокупности должен быть выражен только в единицах, а не в тысячах или в миллионах единиц. Например, подставив в данную формулу общую численность населения региона, выраженную в тысячах человек, мы не получим правильное значение необходимой численности выборки, также выраженное в тысячах человек, как это иногда бывает в других расчетах. Результат вычислений будет неверен.