Сила давления жидкости на плоскую стенку произвольной формы

Пусть имеется фигура произвольной формы площадью со в плоскости Оl, наклоненной к горизонту под углом α (рис. 3.17).

Для удобства вывода формулы для силы давления жидкости на рассматриваемую фигуру повернем плоскость стенки на 90° вокруг оси 01 и совместим ее с плоскостью чертежа. Выделим на рассматриваемой плоской фигуре на глубине h от свободной поверхности жидкости элементарную площадку dω. Тогда элементарная сила, действующая на площадку dω, будет

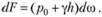
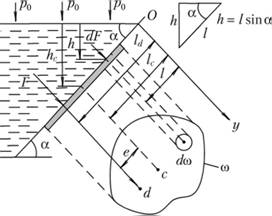
Рис. 3.17. Схема к определению силы давления жидкости на плоскую стенку

Интегрируя последнее соотношение, получаем суммарную силу давления жидкости на плоскую фигуру

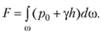
Учитывая, что 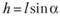, получаем

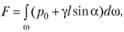
или

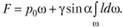
Последний интеграл равен статическому моменту площадки со относительно оси Оу, т.е.

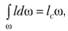
где lС – расстояние от оси Оу до центра тяжести фигуры. Тогда

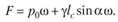
Так как 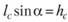, то

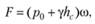
т.е. суммарная сила давления на плоскую фигуру равна произведению площади фигуры на гидростатическое давление в ее центре тяжести.

Точка приложения суммарной силы давления (точка d, см. рис. 3.17) называется центром давления. Центр давления находится ниже центра тяжести плоской фигуры на величину е. Последовательность определения координат центра давления и величины эксцентриситета изложена в параграфе 3.13.

В частном случае вертикальной прямоугольной стенки получим (рис. 3.18)

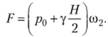
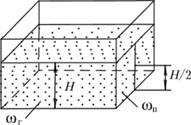
Рис. 3.18. Схема к определению силы давления жидкости на горизонтальную и вертикальную стенку

В случае горизонтальной прямоугольной стенки будем иметь

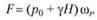(3.31)

Гидростатический парадокс

Формула для силы давления на горизонтальную стенку (3.31) показывает, что суммарное давление на плоскую фигуру определяется лишь глубиной погружения центра тяжести и площадью самой фигуры, но не зависит от формы того сосуда, в котором находится жидкость. Поэтому, если взять ряд сосудов, различных по форме, но имеющих одинаковую площадь дна ωг и равные уровни жидкости H, то во всех этих сосудах суммарное давление на дно будет одинаковым (рис. 3.19). Гидростатическое давление обусловлено в данном случае силой тяжести, но вес жидкости в сосудах разный.

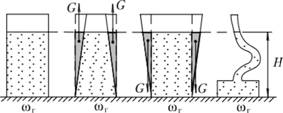
Рис. 3.19. Схема к объяснению гидростатического парадокса

Возникает вопрос: как же различный вес может создать одинаковое давление на дно? В этом кажущемся противоречии и состоит так называемый гидростатический парадокс. Раскрытие парадокса заключается в том, что сила веса жидкости действует в действительности не только на дно, но еще и на другие стенки сосуда.

В случае расширяющегося кверху сосуда очевидно, что вес жидкости больше силы, действующей на дно. Однако в данном случае часть силы веса действует на наклонные стенки. Эта часть есть вес тела давления.

В случае сужающегося к верху сосуда достаточно вспомнить, что вес тела давления G в этом случае отрицателен и действует на сосуд вверх.

Центр давления и определение его координат

Точку приложения суммарной силы давления называют центром давления. Определим координаты центра давления ld и yd (рис. 3.20). Как известно из теоретической механики, при равновесии момент равнодействующей силы F относительно некоторой оси равен сумме моментов составляющих сил dF относительно той же оси.

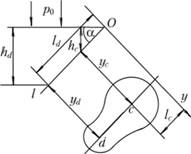
Рис. 3.20. Схема к определению координат центра давления

Составим уравнение моментов сил F и dF относительно оси Оу:

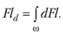
Силы F и dF определим по формулам

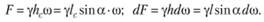
Тогда

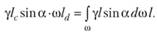
Разделив последнее соотношение на γ и sinα, получим

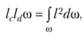
где 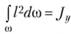– момент инерции площади фигуры относительно оси Оу.

Отсюда

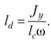
Заменив Jy по известной из теоретической механики формуле 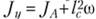, где Jc – момент инерции площади фигуры относительно оси, параллельной Оу и проходящей через центр тяжести, получим

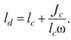
Из этой формулы следует, что центр давления всегда расположен ниже центра тяжести фигуры на расстоянии 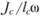. Это расстояние называется эксцентриситетом и обозначается буквой е.

Координата yd находится из аналогичных соображений:

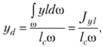
где 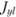– центробежный момент инерции той же площади относительно осей Оу и Ol. Если фигура симметрична относительно оси, параллельной оси Ol (см. рис. 3.20), то, очевидно, 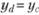, где ус – координата центра тяжести фигуры.