Лекция 8. СЕТЕВОЙ АНАЛИЗ И КАЛЕНДАРНОЕ ПЛАНИРОВАНИЕ ПРОЕКТА

Изучив материал главы, студент должен:

знать

• какую роль играет сетевое и календарное планирование в управлении проектом;

• основные принципы сетевого планирования;

• основные инструменты сетевого и календарного планирования;

уметь

• строить сетевые графы проекта;

• определять на основании сетевых графов длительность проекта, его критические операции;

• определять резервы времени для каждой операции;

• определять длительность выполнения операций на основе метода PERT;

• распределять ресурсы проекта с учетом их дефицитности;

владеть

• общепринятыми методами сетевого анализа;

• навыками составления сетевых графов, диаграмм Ганта;

• навыками определения длительности проекта;

• навыками формирования расписания проекта.

Ключевые термины: сетевой анализ, календарное планирование,

сетевой граф, критический путь, резерв времени, диаграмма Ганта.

Функции сетевого анализа в планировании проекта

Для успешной реализации проекта необходимо составить его реалистичное расписание, позволяющее распределить ресурсы и контролировать ход выполнения проекта. С этой целью составляются и анализируются сетевые модели проекта, определяющие конкретные взаимосвязи между задачами (пакетами работ). На основе сетевого анализа можно определить вероятную продолжительность выполнения работ, их стоимость, возможные размеры экономии времени или денежных средств, а также то, выполнение каких операций можно отложить без ущерба для расписания проекта в целом, а какие являются критическими, т.е. их задержка означает срыв сроков реализации всего проекта. Сетевое планирование является также базой для распределения ресурсов проекта, в том числе дефицитных.

Сетевой анализ осуществляется в последовательности, приведенной на рис. 8.1.

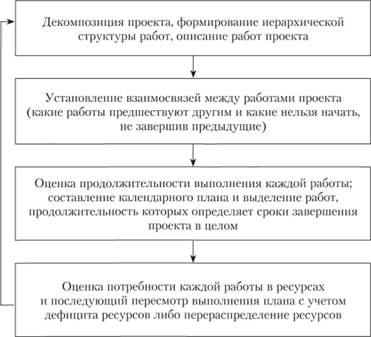
Рис. 8.1. Последовательность этапов формирования расписания проекта

Первые три этапа составляют сущность сетевого анализа, а последний – календарного планирования. Как правило, процесс проходит несколько итераций.

Первый этап был описан нами в гл. 7. На втором этапе устанавливаются взаимосвязи между работами проекта, которые в рамках сетевого анализа называются операциями.

Можно выделить следующие типы зависимостей.

1. Обязательные зависимости – зависимости, которые внутренне (физически) присущи выполняемым работам (например, при строительстве дома нельзя настелить крышу раньше, чем будут возведены стены).

2. Зависимости по усмотрению – определяются командой проекта на основе их предпочтений или общепринятой практики. Такие зависимости следует строго документировать во избежание нарушения сроков реализации проекта.

3. Внешние зависимости – определяют взаимосвязи проектных и непроектных работ.

Для установления логических взаимосвязей между операциями составляется таблица предшествования, в которой каждой операции сопоставляется непосредственно предшествующая (предшествующие, если их несколько) операция.

Пример 8.1

Компания АВС заключила контракт на производство партии станков, которые должны быть использованы для производства определенного типа деталей. Ниже приведена таблица предшествования, где перечислены операции, которые необходимо выполнить в процессе разработки и производства этих станков.

Код операции	Описание операции	Непосредственно предшествующая операция
А	Составление сметы затрат проекта	–
В	Согласование сметы затрат	А
С	Покупка собственного оборудования	В
D	Подготовка конструкторской документации	В
Е	Строительство цеха	D
F	Монтаж оборудования	С, Е
G	Испытания оборудования	F
Н	Определение типа модели	D
I	Проектирование внешнего корпуса	D
J	Создание внешнего корпуса	H, I
К	Конечная сборка	G, J
L	Контрольная проверка	К

Инструментом сетевого анализа выступают сетевые графы. Существуют различные типы сетевых графов, но наиболее часто используются стрелочные графы.

В стрелочных графах каждая операция обозначается буквой и представлена стрелкой, каждая операция начинается и заканчивается событием, имеющим определенный номер (рис. 8.2).

Рис. 8.2. Изображение операции на стрелочном сетевом графе

В процессе планирования следует учитывать, что многие операции будут выполняться одновременно, следовательно, одному событию могут соответствовать (начинаться или заканчиваться им) несколько операций. Событие не считается свершившимся, пока не закончатся все входящие в него операции. Операция, выходящая из некоторого события, не может начаться, пока не будут закончены все входящие в него операции. Так, на рис. 8.3 операция С не может быть начата до момента, пока не будут окончены работы А и В.

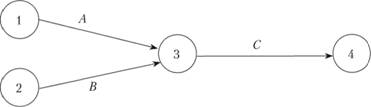
Рис. 8.3. Изображение логической последовательности операций в стрелочном графе

Иногда для изображения логической последовательности операций в графы вводятся так называемые фиктивные операции, изображаемые пунктирными стрелками и имеющие нулевую продолжительность. Они используются тогда, когда необходимо отразить, что некоторое событие не может появиться раньше другого события, а с помощью обычных стрелок, соответствующих действительным операциям, этого сделать нельзя. Такая ситуация показана на рис. 8.4. Операция С не может начаться раньше, чем завершится операция А, а работу D нельзя начинать раньше, чем завершатся операции А и В. События принято нумеровать так, чтобы номер конечного события был больше номеров предшествующих событий.

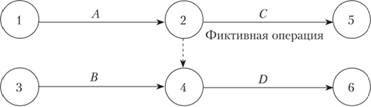
Рис. 8.4. Стрелочный граф с фиктивной логической операцией

После того как на основе таблицы предшествования строится стрелочный граф, он, как правило, пересматривается с целью исключения ненужных фиктивных операций. Это можно сделать на основе следующего принципа – если единственная операция, выходящая из некоторого события, фиктивная, скорее всего, без нее можно обойтись.

Сетевой граф должен начинаться с единственного начального события (с него начинаются все операции, не имеющие предшествующих) и заканчиваться единственным конечным событием.

Пример 8.2

Построим сетевой граф для таблицы предшествования из примера 8.1.

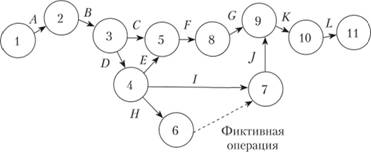
После установления последовательности и логической взаимосвязи операций оценивается их продолжительность, а следовательно, и продолжительность всего проекта.

Помимо стрелочных графов, используют также вершинные графы (диаграммы предшествования), где узлы содержат операции проекта, а стрелки между ними характеризуют продолжительность операций (рис. 8.5).

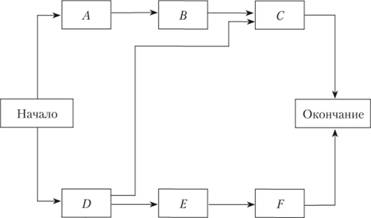
Рис. 8.5. Пример вершинного графа