Прогнозный анализ
Метод экстраполяции. Этот метод анализа основан на результатах ретроспективного анализа. Получив уравнение тренда, можно определить прогнозные оценки результативного показателя на будущие периоды.
Пример
В результате изучения динамики показателя объема продаж за 12 кварталов было получено следующее выражение тренда:
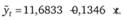
Необходимо определить прогнозное значение объема продаж для 13-го и 14-го кварталов.
Выполнение примера достигается следующим расчетом:
• прогноз для 13-го квартала:
• прогноз для 14-го квартала
На рис. 9.1 экстраполяция выделена линией как продолжение тренда за пределами рассматриваемых 12 кварталов.
Рис. 9.1. Графическое изображение метода экстраполяции
Такой подход к прогнозированию показателей хозяйственной деятельности отличается простотой и наглядностью. Но он не отражает колебания, происходящие в развитии предприятия. Это достигается использованием адаптивных моделей.
Учет сезонной составляющей при экстраполяции данных. Рассчитаем компоненты аддитивной модели по условиям данных таблицы.
1. Производится выравнивание значений объема продаж при помощи скользящей средней и находятся оценки сезонной компоненты как разность между фактическим объемом продаж и центрированными скользящими средними.
|
Квартал |
Объем продаж |
Четырехквартальные скользящие средние |
Оценка сезонной компоненты |
|
|
нецентрированные |
центрированные |
|||
|
1 |
2 |
3 |
4 |
5 |
|
1 |
9,7 |
|||
|
2 |
9,9 |
|||
|
3 |
11,4 |
11,0 |
11,6 |
-0,2 |
|
4 |
12,9 |
12,3 |
12,5 |
0,4 |
|
5 |
14,9 |
12,8 |
12,7 |
2,2 |
|
6 |
12,1 |
12,7 |
12,3 |
-0,2 |
|
7 |
11,0 |
11,9 |
11,0 |
0 |
|
8 |
9,8 |
10,2 |
9,7 |
0,1 |
|
9 |
7,9 |
9,2 |
9,0 |
-1,1 |
|
10 |
8,2 |
8,9 |
9,2 |
-1 |
|
11 |
9,9 |
9,5 |
||
|
12 |
12,0 |
|||
2. Производится корректировка сезонной компоненты для того, чтобы ее сумма значений по всем кварталам была равной нулю.
|
Показатели |
Номер квартала |
||||
|
I |
II |
III |
IV |
||
|
Год |
1 |
-0,2 |
0,4 |
||
|
2 |
2,2 |
0,2 |
0 |
0,1 |
|
|
3 |
-1,1 |
-1 |
|||
|
Итого за квартал |
1,1 |
-0,8 |
-0,2 |
0,5 |
|
|
Среднее значение сезонной компоненты |
0,55 |
-0,4 |
-0,1 |
0,25 |
|
|
Скорректированное значение сезонной компоненты |
0,475 |
-0,475 |
-0,175 |
0,175 |
|
Сумма средних значений сезонной компоненты равна
Корректирующий коэффициент равен 0,3 : 4 = 0,075.
Расчет скорректированных значений сезонной компоненты производится вычитанием корректирующего коэффициента из средних значений сезонной компоненты:
Сумма полученных значений равна нулю:
3. Из каждого уровня исходного временного ряда вычитаем значение скорректированной сезонной компоненты. Полученные значения содержат только трендовую и случайную компоненты:
|
Квартал |
Объем продаж |
Скорректированное значение сезонной компоненты |
Тренд и случайная компонента
|
|
1 |
9,7 |
0,475 |
9,225 |
|
2 |
9,9 |
-0,475 |
10,375 |
|
3 |
11,4 |
-0,175 |
11,575 |
|
4 |
12,9 |
0,175 |
12,725 |
|
5 |
14,9 |
0,475 |
14,425 |
|
6 |
12,1 |
-0,475 |
12,575 |
|
7 |
11,0 |
-0,175 |
11,175 |
|
8 |
9,8 |
0,175 |
9,625 |
|
9 |
7,9 |
0,475 |
7,425 |
|
10 |
8,2 |
-0,475 |
8,675 |
|
11 |
9,9 |
-0,175 |
10,075 |
|
12 |
12,0 |
0,175 |
11,825 |
4. Формируется тренд по линейной зависимости и рассчитывается средняя относительная ошибка аппроксимации:
5. Выполним прогноз на 13-й квартал:
При прогнозе была учтена сезонная компонента, которая в 13-м квартале соответствует значению компоненты первого квартала.
Методика определения сезонной составляющей по мультипликативной модели во многом схожа с алгоритмом расчетов по аддитивной модели. Также определяются центрированные скользящие средние и с их помощью находятся сезонные отклонения. Но при мультипликативной модели сезонные отклонения определяются как частное от деления фактических значений ряда (объем продаж) на соответствующие значения центрированных скользящих средних. Второе отличие заключается в определении скорректированных значений сезонной компоненты. Для исключения искажений тенденции при вычленении сезонных колебаний из исходного ряда необходимо, чтобы сумма средних значений сезонной компоненты была равна не нулю (как в случае аддитивной модели), а количеству сезонов, т.е. четырем. Если это условие не выполняется, вводится поправочный коэффициент (четыре делится на сумму средних значений сезонной компоненты).
Далее каждый уровень исходного ряда делится на соответствующее значение сезонной компоненты и в таблицу будет занесена величина
После этого формируется тренд по линейной зависимости и рассчитывается средняя относительная ошибка аппроксимации.
Адаптивная модель. При краткосрочном прогнозировании более важной является не тенденция развития показателя, а его динамика в последние периоды наблюдений. Поэтому более эффективными при прогнозировании являются адаптивные методы, учитывающие динамическую неравномерность данных. Прогноз строится на основе адаптивной модели, которая постоянно корректируется с появлением новых данных. Это позволяет отражать колебательные (сезонные или циклические) процессы в развитии исследуемого предприятия. Таким образом, адаптивная модель способна оперативно реагировать на изменение условий деятельности путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда. Допустим, что модель находится в некотором состоянии, для которого определены текущие значения ее коэффициентов. На основе этой модели делается прогноз. При поступлении фактического значения оценивается ошибка прогноза (разница между фактическим значением и полученным по модели). Ошибка прогнозирования через обратную связь поступает в модель и учитывается в ней в соответствии с принятой процедурой перехода от одного состояния в другое. В результате производится корректировка параметров, что обеспечивает более высокую согласованность поведения модели с динамикой ряда. Затем рассчитывается прогнозная оценка на следующий момент времени, и весь процесс повторяется вновь.
При построении адаптивных моделей также используется механизм скользящих средних. Однако в отличие от ранее рассмотренных скользящих средних, где всем данным придавался равноправный характер, при адаптивном прогнозировании скользящим средним придаются веса. Так возникает экспоненциальная скользящая средняя, а процесс работы с ней называется экспоненциальным сглаживанием.
Рассмотрим простую модель экспоненциального сглаживания. Прогнозирование значений показателя производится на основе следующей формулы:
где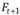 
–новый прогноз (на шаг вперед);
– фактический результат в последний период;
– прогноз в предыдущий период;
α – выбранная константа сглаживания (вес).
Константа сглаживания α – это величина между 0 и 1, которую самостоятельно выбирает аналитик в зависимости от специфики конкретного применения. Если величина константы α выбирается равной нулю, то прогноз на следующий период будет равен прогнозу на текущий период, т.е. полностью основан на данных прошлого периода (при этом в расчет не принимаются наиболее поздние из имеющихся фактических данных). Если константа а принимается равной единице, то данным прошлых периодов не придается никакого значения, и прогноз полностью зависит от фактического спроса на текущий период, так как в подобном случае данные прошлых периодов для составления прогноза отсутствуют. Константа а зависит от степени колебаний уровней динамического ряда. Если колебания незначительны, α принимается на уровне 0,2–0,4. При значительных колебаниях а может составить 0,6–0,8. Поэтому значение константы аналитик принимает самостоятельно, исходя их своего опыта и знаний. Иногда бывает целесообразно попробовать несколько вариантов подбора, чтобы определить, какое значение α в большей степени отвечает поставленной задаче.
Пример
В таблице приведен прогноз объема продаж, включающий два варианта расчета при α = 0,4 и при α = 0,6.
|
Квартал |
Объем продаж, тыс. руб. |
Константа сглаживания |
|
|
α = 0,4 |
α = 0,6 |
||
|
1 |
9,7 |
10,0 |
10,0 |
|
2 |
9,9 |
9,88 |
9,82 |
|
3 |
11,4 |
9,884 |
9,868 |
|
4 |
12,9 |
10,1872 |
10,7872 |
|
5 |
14,9 |
10,72976 |
12,05488 |
|
6 |
12,1 |
11,56381 |
13,76195 |
|
7 |
11,0 |
11,67105 |
12,76478 |
|
8 |
9,8 |
11,53684 |
11,70591 |
|
9 |
7,9 |
11,18947 |
10,56236 |
|
10 |
8,2 |
10,53158 |
8,964946 |
|
11 |
9,9 |
10,06526 |
8,505978 |
|
12 |
12,0 |
10,03221 |
9,342391 |
|
13 |
Прогноз |
10,42577 |
10,93696 |
При значении константы 0,4 результаты экспоненциального сглаживания совпадают с прогнозом примера 5, в котором была учтена сезонная компонента.
Прогнозный анализ можно проводить по отношению к большинству показателей хозяйственной деятельности предприятия.