Порядок построения фронтальных диметрических проекций

Рассмотрим порядок построения фронтальной диметрической проекции предмета, три вида которого приведены на рис. 3.5, а.

Вначале проводят оси (рис. 3.5, б). Затем в плоскости xOz строят изображение передней грани (рис. 3.5, в). При этом все отрезки вертикальных прямых линий проводят параллельно оси 2, а отрезки горизонтальных прямых – параллельно оси х. Чтобы выполнить построение, от точки О по оси х откладывают ширину предмета – размер 50 мм. Затем из конца отложенного отрезка восставляют перпендикуляр и откладывают на нем размер высоты (90 мм), так как высота параллельна оси z. Верхняя сторона фигуры параллельна нижней, поэтому из конца полученного отрезка проводят прямую, параллельную оси х, и откладывают на ней соответствующий размер (20 мм). Из полученной точки проводят линию, параллельную оси z. От точки О по оси z откладывают высоту, равную 40 мм, и из полученной точки проводят линию, параллельную оси х. Таким образом, передняя грань предмета изображена.

Рис. 3.5. Порядок построения фронтальной диметрической проекции предмета

Затем проводят линии, соответствующие ребрам, перпендикулярным передней грани призмы. Их вычерчивают параллельными оси у.

Ось у показывает на чертеже направление, перпендикулярное плоскости xOz. Поэтому толщину предмета откладывают параллельно оси у, т.е. под углом 45°. Длина всех ребер одинакова, так как передняя грань параллельна задней. На всех прямых, расположенных под углом 45°, нужно было бы отложить одинаковые отрезки длиной по 60 мм. Но так как по оси у все размеры сокращают наполовину, то откладывают по 30 мм (рис. 3.5, д). Полученные точки последовательно соединяют прямыми (рис. 3.5, е).

Построение легко проверить. Ребра, ограничивающие заднюю грань, параллельны соответствующим ребрам передней грани. Следовательно, и на чертеже они должны быть взаимно параллельны. Если это не получилось, проекция построена неверно.

Затем обводят видимый контур и наносят размеры (рис. 3.5, ж). Размерные и выносные линии в наглядных изображениях располагают параллельно аксонометрическим осям.

Рассмотрим построение фронтальной диметрической проекции правильной треугольной призмы, два вида которой даны на рис. 3.6, а. Построение проведено следующим образом. Вычерчены оси (рис. 3.6, б). Затем построена фигура основания призмы – равносторонний треугольник (рис. 3.6, в). Для этого по оси х в обе стороны от точки О отложено по половине длины стороны основания: отрезки прямых по 40 мм. От точки О по оси у отложен отрезок, равный половине высоты треугольника. Три полученные точки соединены прямыми, которые образовали аксонометрическое изображение равностороннего треугольника. Затем из вершин полученного треугольника проведены линии, изображающие вертикальные ребра призмы (рис. 3.6, г). На одном из них отложена высота вычерчиваемого тела, равная 100 мм. Ребра верхнего основания проведены параллельно соответствующим ребрам нижнего основания, как это имеет место в действительности. Невидимое ребро проведено штриховой линией, обведен видимый контур и проставлены размеры (рис. 3.6, д).

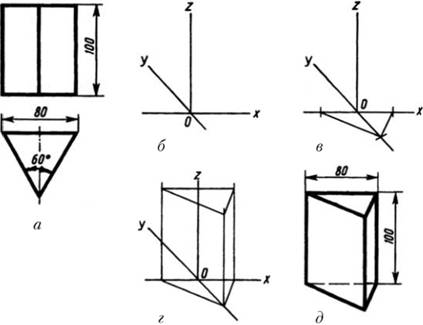
Рис. 3.6. Последовательность построения фронтальной диметрической проекции треугольной призмы

Построение фронтальной диметрической проекции правильной шестиугольной призмы выполнено так (рис. 3.7, а). В окружность с центром в точке О пересечения осей вписан шестиугольник (рис. 3.7, б) со стороной, равной 40 мм. Ребра проведены под углом 45°, т. е. параллельно оси у (рис. 3.7, в). На одном из ребер отложен сокращенный вдвое размер высоты – 50 мм, и на этом расстоянии проведены параллельные сторонам шестиугольника прямые, изображающие видимые ребра основания призмы (рис. 3.7, г), затем обведен видимый контур и поставлены размеры (рис. 3.7, д).

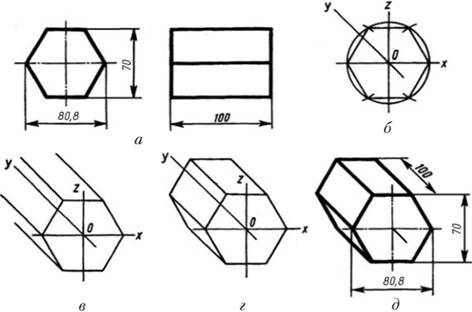
Рис. 3.7. Последовательность построения фронтальной диметрической проекции шестиугольной призмы

Правильную четырехугольную пирамиду во фронтальной диметрической проекции, два вида которой представлены на рис. 3.8, а, легко изобразить, начиная с фигуры основания. Для этого откладывают по оси х полный размер стороны основания пирамиды, а по оси у – размер, сокращенный вдвое (рис. 3.8, б). Через полученные точки проводят отрезки прямых, параллельные осям х и у, получая фронтальную диметрическую проекцию квадрата, являющегося основанием пирамиды.

По оси z от точки О откладывают высоту пирамиды и полученную точку соединяют с вершинами основания (рис. 3.8, в). Затем обводят видимый и невидимый контуры, наносят размеры (рис. 3.8, г).

Рис. 3.8. Последовательность построения фронтальной диметрической проекции четырехугольной пирамиды

Как видно из построения, высота пирамиды совпадает с осью z. Такое положение изображаемого объекта, когда его высота, сторона основания, боковые ребра и другие элементы параллельны осям х, у, z, соответственно является предпочтительным, так как это облегчает построение аксонометрических проекций.

Рассмотрим вычерчивание наглядного изображения детали, имеющей выступ (рис. 3.9, а). В этом случае важно выбрать правильный порядок выполнения чертежа. Построение не следует начинать с выступа, лучше сначала вычертить тело детали, а затем пристроить выступ, как это сделано на рис. 3.9, б – д.

Рис. 3.9. Последовательность построения фронтальной диметрической проекции детали, имеющей выступ

Рассмотрев несколько случаев построения фронтальных диметрических проекций разных деталей, можно сделать вывод, что выбор последовательности построения наглядного изображения зависит от формы детали. В одних случаях целесообразно начинать чертить с изображения передней грани, в других – с основания предмета, иногда – с задней грани. Но во всех случаях необходимо придерживаться следующих правил:

• ребра, перпендикулярные плоскости хОу, проводить параллельно оси у,

• параллельные элементы предметов сохранять параллельными и в аксонометрической проекции;

• все отрезки прямых линий, которые в натуре имели направление, параллельное осям х, у или z, оставлять параллельными тем же осям и в наглядном изображении;

• располагать изображаемый объект целесообразно так, чтобы основные его элементы совпадали с осями проекций.