Полуэмпирические теории турбулентности
Величина
в формуле (6.11) обусловлена пульсационными добавками скорости. Для ее определения необходимо иметь зависимость этих добавок от осредненных характеристик потока. Вследствие хаотичного характера турбулентного потока для получения таких зависимостей необходимо применять статистические методы, на которых основаны так называемые статистические теории турбулентности. Однако основанные на этих теориях зависимости оказываются весьма сложными, и поэтому они не получили распространения в инженерной практике при решении задач о распределении скоростей и потерях энергии в турбулентном потоке.
Для количественного описания турбулентного движения используются так называемые полуэмпирические теории турбулентности, основанные на упрощенных моделях турбулентного потока.
Основной частью таких теорий является предположение о том, что касательное напряжение, вызванное турбулентным перемешиванием, можно описать в виде, аналогичном закону вязкости Ньютона
где 
– динамический коэффициент турбулентной вязкости. Этот коэффициент имеет ту же размерность, что и обычный динамический коэффициент вязкости
при ламинарном движении, но отличается от него тем, что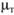
не является свойством жидкости, а зависит от интенсивности турбулентного перемешивания.
Различные полуэмпирические теории турбулентности отличаются использованием различных выражений для турбулентной вязкости
. Наиболее распространена из них теория Прандтля.
Согласно этой теории на различных расстояниях от стенки величины
и
имеют различные значения. Вдали от стенки градиенты скорости малы и, следовательно, вязкостные напряжения
значительно меньше турбулентных
, и наоборот, вблизи стенок преобладают вязкостные напряжения. На этом основании поток разделяется на две области: ламинарный гидродинамический пограничный слой (ламинарный подслой) у стенок, где движение ламинарное и оно формируется исключительно под действием сил вязкости, и турбулентное ядро, где влиянием вязкости можно пренебречь.
Для величины касательного напряжения в ядре потока
принимается выражение
Для установления связи между т и осредненными скоростями движения Л. Прандтль исходил из следующей схемы пульсационного движения в осредненном плоскопараллельном турбулентном потоке (рис. 6.15).
Рис. 6.15. Схема к объяснению полуэмпирической теории турбулентности Прандтля
В турбулентном потоке возникают жидкие комки (моли). Каждый из таких комков обладает собственной скоростью и движется на протяжении некоторого расстояния l в поперечном направлении в виде неразрывного целого с сохранением составляющей скорости и вдоль оси х.
После того как жидкий комок (моль) пройдет некоторое расстояние l, он попадает в другой слой жидкости, где целиком смешивается с этим слоем и приобретает скорость этого слоя.
Величину пути l, пройденного молем в поперечном направлении вплоть до потери им его индивидуальных особенностей, Л. Прандтль назвал путем перемешивания.
Предположим, что такой моль жидкости перешел из слоя 2 в слой 1 (см. рис. 6.15). Так как в слое 2 моль в среднем во времени имел скорость
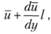
а в слое 1 скорость равна
, то естественно предположить, что возникающая в слое 1 пульсация
(6.12)
т. е. величина пульсации равна привнесенному в слой возмущению скорости.
Величину поперечной пульсации
Прандтль принимает пропорциональной продольной пульсации 
:
(6.13)
где k – коэффициент пропорциональности.
Так как продольная пульсация возникает благодаря поперечной, то естественно положить, что
и
пропорциональны (если 
, то и 
; чем больше 
, тем больше и продольные пульсации
).
Кроме того,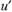
и
разного знака. Действительно, положительная пульсация
приводит к отрицательной пульсации
, так как моль переходит от слоя с меньшей скоростью в слой с большей скоростью. И наоборот, отрицательная пульсация 
вызывает положительную пульсацию
, так как жидкость переходит из верхнего слоя с большей скоростью в нижний. Из формулы (6.13) с учетом равенства (6.12) следует
Тогда турбулентное напряжение можно представить в виде
или
Здесь коэффициент пропорциональности k внесен в величину l, где l по-прежнему характеризует путь молярного перемешивания, но с точностью до постоянного множителя.
Таким образом, избавление от пульсационных добавок приводит к появлению новой функции l (путь перемешивания), которая должна находиться из опыта эмпирически. Поэтому и теория Прандтля названа полуэмпирической.
В дальнейшем для простоты знак осреднения над величинами писать не будем, т.е. будем иметь дело только с осредненными величинами. Формулу для
можно записать в виде
Вводя динамический коэффициент турбулентной вязкости 
(коэффициент турбулентного обмена), получаем
,
где
Можно ввести кинематический коэффициент турбулентной вязкости
Суммарное касательное напряжение от молекулярного и молярно-турбулентного трения будет
где 
не является физической постоянной жидкости, а есть функция ее движения – скорости и.
Как показывает опыт, коэффициент 
резко меняется но сечению трубы от нуля у стенки (так как там нет перемешивания) до некоторого максимума на расстоянии 
трубы и до некоторого минимума на оси трубы. В области развитого турбулентного движения 
значительно больше величины 
. В связи с этим всюду в потоке, за исключением области, непосредственно прилегающей к стенке, вязкими напряжениями по сравнению с турбулентными можно пренебречь.
Эпюра касательных напряжений в турбулентном потоке в круглой трубе имеет вид, показанный на рис. 6.16.
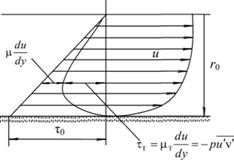
Рис. 6.16. Эпюры скоростей и касательных напряжений в турбулентном потоке