Основы выборочного метода контроля

Понятие доверительного интервала. При опенке выборочных статистических характеристик всегда возникает ошибка, связанная с тем, что объем выборки меньше объема генеральной совокупности.

Отрезок на числовой оси, откладываемый от влево и вправо, в который с определенной вероятностью попадает истинное значение статистической характеристики тx, называется доверительным интервалом (рис. 10.4). Вероятность, с которой истинное значение статистической характеристики попадает в заданный интервал, называется доверительной вероятностью.

Рис. 10.4. Доверительный интервал

Вероятность попадания случайной величины х, распределенной по нормальному закону, в котором функция плотности распределения f(x) описывается зависимостью

в интервале [х – L; х + L] может быть определена по формуле

Учитывая, что Ф(1) = 1 – Ф(–1), сделаем дальнейшие преобразования:

Эта вероятность называется доверительной и обозначается β, интервал [х – L; х + L] также называется доверительным.

В практических расчетах половина длины доверительного интервала измеряется числом средних квадратических отклонений. Это число обозначается и называется коэффициентом Стьюдента. В задачах, где определяется доверительный интервал для математического ожидания, он рассчитывается по формуле

где – коэффициент Стьюдента (табл. 10.5), – стандартное отклонение.

Табличная величина зависит от объема выборочной совокупности и доверительной вероятности.

Доверительный интервал для математического ожидания определяется по формуле

Доверительный интервал для любого случайного значения определяется по формуле

Таблица 10.5

Таблица значений коэффициентов Стьюдента tβ в зависимости от значений ß доверительной вероятности и объема выборки n

п – ß

0,4

0,5

0,6

0,7

0,8

0,9

0,95

0,98

0,99

0,999

3

0,617

0,816

1,061

1,336

1,886

2,920

4,30

6,96

9,92

31,60

4

0,584

0,765

0,978

1,250

1,638

2,350

3,18

4,54

5,84

12,94

5

0,569

0,741

0,941

1,190

1,533

2,130

2,77

3,75

4,60

8,61

6

0,559

0,727

0,920

1,156

1,476

2,020

2,57

3,36

4,03

6,86

7

0,553

0,718

0,906

1,134

1,440

1,943

2,45

3,14

3,71

5,96

8

0,549

0,711

0,896

1,119

1,415

1,895

2,36

3,00

3,50

5,40

9

0,546

0,706

0,889

1,108

1,397

1,860

2,31

2,89

3,36

5,04

10

0,543

0,703

0,884

1,100

1,383

1,833

2,36

2,82

3,25

4,78

11

0,542

0,700

0,879

1,093

1,372

1,812

2,23

2,76

3,17

4,59

12

0,540

0,697

0,876

1,088

1,363

1,796

2,20

2,72

3,11

4,49

13

0,539

0,695

0,873

1,083

1,356

1,782

2,18

2,68

3,06

4,32

14

0,538

0,694

0,870

1,079

1,350

1,771

2,16

2,65

3,01

4,22

15

0,537

0,692

0,862

1,076

1,345

1,761

2,14

2,62

2,98

4,14

16

0,536

0,691

0,866

1,074

1,341

1,753

2,13

2,60

2,95

4,07

17

0,535

0,690

0,865

1,071

1,337

1,746

2,12

2,58

2,92

4,02

18

0,534

0,689

0,863

1,069

1,333

1,740

2,11

2,57

2,90

3,96

19

0,534

0,688

0,862

1,067

1.330

1,734

2,10

2,55

2,88

3,92

20

0,533

0,688

0,861

1,066

1,328

1,729

2,09

2,54

2,86

3,88

21

0,533

0,687

0,860

1,064

1,325

1,725

2,09

2,53

2,84

3,85

22

0,532

0,686

0,859

1,063

1,323

1,721

2,08

2.:,2

2,83

3,82

23

0,532

0,686

0,858

1,061

1,321

1,717

2,07

2,51

2,82

3,79

24

0,532

0,685

0,858

1,060

1,319

1,714

2,07

2,50

2,81

3,77

25

0,531

0,685

0,857

1,059

1,318

1,711

2,06

2,49

2,80

3,74

26

0,531

0,684

0,856

1,058

1,316

1,708

2,06

2,48

2,79

3,72

27

0,531

0,684

0.856

1,058

1,315

1,706

2,06

2,48

2,79

3,71

28

0,531

0,684

0,855

1,057

1,314

1,703

2,05

2,47

2,77

3,69

29

0,530

0,683

0,855

1,056

1,313

1,701

2,05

2,47

2,76

3,67

30

0,530

0,683

0,854

1,055

1,311

1,699

2,04

2,46

2,76

3,66

31

0,530

0,683

0,854

1,055

1,310

1,697

2,04

2,46

2,75

3,65

40

0,529

0,681

0,851

1,050

1,303

1,684

2,02

2,42

2,70

3,55

60

0,527

0,679

0,848

1,046

1,296

1,671

2,00

2,39

2,66

3,46

120

0,526

0,677

0,845

1,041

1,289

1,658

1,98

2,36

2,62

3,37

0,524

0,674

0,842

1,036

1,282

1,645

1,96

2,33

2,58

3,29

Таблицы значений можно также использовать для получения односторонних оценок, характеризующих верхнее (ВГ) и нижнее (НГ) гарантированные значения показателя:

Гарантия для односторонней оценки равна

Примечание: на практике целесообразно принимать ß = 0,7, что обеспечивает Р(ВГ) = 0,85.

Формирование выборок. Выборочный метод подразумевает обследование некоторого количества единиц, специальным образом отобранных из генеральной совокупности.

В зависимости от способа формирования различают: собственно случайные, механические, типические и серийные выборки.

Собственно случайная выборка – члены генеральной совокупности включаются в выборку случайным образом. Эта выборка может быть с повторным или бесповторным отбором.

Механическая выборка – члены генеральной совокупности выбираются через определенный интервал (через 5, 10 и т.п.).

Типическая выборка – члены генеральной совокупности предварительно разбиваются на непересекающиеся группы, затем от каждой группы образуются собственно случайные выборки и включаются в собственную выборочную совокупность.

Серийная выборка – генеральная совокупность разбивается на группы (серии), затем из групп (серий) отбираются некоторые полностью и включаются в выборочную совокупность.

Определение объема выборки. Выборочный метод позволяет значительно сократить время на контроль и получение основных статистических характеристик, по приводит к появлению ошибок и уменьшению гарантии получения истинных характеристик генеральной совокупности.

Предельной ошибкой выборки при нахождении среднего значения называется наибольшее отклонение выборочной средней от математического ожидания генеральной совокупности, которое может быть допущено с заданной доверительной вероятностью.

При решении задачи определения выборочной средней в случае использования бесповторной выборки предельная ошибка L рассчитывается по формуле

где n' – объем выборки при бесповторном отборе, N – объем генеральной совокупности.

При определении выборочной доли ω предельная ошибка определяется следующим образом:

– для повторной выборки:

– для бесповторной выборки:

Приведенные выражения позволяют определить минимальное значение объема выборки. Так, выше было показано, что для повторной выборки

Тогда .

Откуда .

Для бесповторной выборки

Так как для повторной выборки ,

то

В случае разделения генеральной совокупности на два класса изделий (например, бездефектных и дефектных) доли их в генеральной совокупности N составляют соответственно Р (число т) и q (N – т). Доля бездефектных изделий ω = т/п.

Математическое ожидание появления бездефектного изделия (дискретной случайной величины) составляет тх = 1Р + 0q, а дисперсия

Следовательно

Тогда для повторной выборки

Если для генеральной совокупности Р и q неизвестны, то Р может быть заменена на выборочную долю ω:

При бесповторном отборе размер выборки п определяется путем преобразования:

Откуда

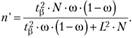
Примечание: если значение выборочной доли со заранее неизвестно, то со принимают равной 0,5. Тогда ω (1 – ω) = 0,25.

ПРИМЕР

Каковы должны быть объемы повторной и бесповторной выборок из совокупности N = 8000 изделий, чтобы с гарантией ß = 0,95 не допустить ошибку в определении доли дефектных изделий, большую, чем 0,02.

Для N = 8000 π ß = 0,95 по табл. 8.5 находим Поскольку заранее доля дефектных изделий неизвестна, то принимаем ω = 0,5. Предельная ошибка L = 0,02.

Для повторной выборки

Для бесповторной выборки

Если принять L = 0,04 (т.е. увеличить предельную ошибку вдвое), то для повторной выборки необходимый объем составит п = 600, а для бесповторной п' = 559.