Лекция 4. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ЗАВИСИМОСТИ ТЕОРИИ ВЗРЫВЧАТЫХ ПРЕВРАЩЕНИЙ
В главе рассматриваются вопросы теории взрывчатых превращений, происходящих при взрыве конденсированных взрывчатых веществ, а также при детонации газовых систем. Для более полного понимания процессов действия взрыва на среду приводятся основные математические зависимости и положения теории механики сплошной среды и пластичности. Приводятся основные типы и группы взрывчатых веществ. Дается определение энергии и мощности взрыва.
Приведены математические зависимости и отличительные особенности детонации газов, условия протекания химических реакций при детонации газов и зависимости, характеризующие пределы распространения детонации. Рассматриваются основные особенности действия взрыва в различных средах. Представлены зависимости, характеризующие формирование основных параметров ударной волны.
В результате усвоения материала данной главы обучаемые должны знать:
а) механизм и условия возникновения взрыва;
б) процессы, сопровождающие возбуждение химических превращений по слою взрывчатого вещества ударной волной;
в) основные положения теории механики сплошной среды и механизм действия продуктов взрыва на окружающую среду;
г) типы взрывчатых веществ и их основные характеристики: энергия взрыва, мощность взрыва;
д) основные закономерности и отличительные особенности, происходящие при детонации газов;
е) условия протекания химических реакций при детонации и пределы распространения детонации, их основные математические зависимости;
ж) характер формирования ударной волны, основные параметры ударной волны и их характеристики;
з) отличительные особенности образования ударной волны в воде;
и) характер действия взрыва в неограниченной и ограниченной твердых средах;
к) характер и механизм образования кумулятивного эффекта и формирование кумулятивной струи;
уметь:
а) проводить расчеты необходимого количества взрывчатых веществ для расчистки завалов и рядовых заторов;
б) проводить оценку поражающих факторов ударной волны, образующихся при взрыве конденсированных взрывчатых веществ и детонации взрывоопасных газовых систем;
владеть:
а) методами расчета и прогнозирования зон поражения, образующихся при взрыве топливо-воздушных систем и взрыве конденсированных взрывчатых веществ;
б) методами расчета сейсмической зоны, зоны разрушения и зоны разлета осколков, образующихся при взрыве конденсированных взрывчатых веществ, заключенных в оболочку.
Некоторые положения механики сплошной среды и пластичности
Чтобы фундаментально представлять механизм действия взрыва на среду, вкратце познакомимся с основными положениями теории механики сплошной среды и пластичности.
Понятие тензора деформации
Положение каждой точки тела определяется ее радиус-вектором  с компонентами x1 = x, x2 = у, x3 = z в некоторой системе координат.
с компонентами x1 = x, x2 = у, x3 = z в некоторой системе координат.
Под действием приложенных сил всякое тело деформируется, меняет свои форму и объем.
И радиус-вектор после приложения силы будет менять свое значение на  .
.
Вектор  называется смещением.
называется смещением.
Квадрат расстояния между двумя точками после деформации (dl) равен
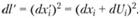 (4.1)
(4.1)
С учетом того, что, выражение для квадрата
расстояния можно записать  следующим образом:
следующим образом:

И окончательно вектор смещения
 (4.2)
(4.2)
Это выражение называется тензором деформации.
В механике сплошной среды принято различать деформации, связанные с изменением объема, и деформации формоизменения, или сдвига.
С этой целью тензор деформации удобно представить в виде
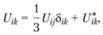 (4.3)
(4.3)
где δik – единичный тензор, компоненты которого равны 1 при i = k и нулю при i ¹ k. Шаровой тензор  соответ
соответ
ствует объемному расширению или сжатию.
Тензор  называется девиатором деформации. Он характеризует изменение формы элемента среды вследствие сдвигов. На площадках, расположенных под углом 45° к главным осям тензора деформации, среда подвержена максимальным главным сдвигам:
называется девиатором деформации. Он характеризует изменение формы элемента среды вследствие сдвигов. На площадках, расположенных под углом 45° к главным осям тензора деформации, среда подвержена максимальным главным сдвигам:
 (4.4)
(4.4)
где ε1, ε2, ε3 – главные изменения.
Для любого симметричного тензора (х, у, z) существуют три величины, которые не меняются при преобразовании координат:
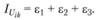 (4.5)
(4.5)
Они называются соответственно линейным, квадратным и кубическим инвариантами тензора.
Отсюда получается интенсивность деформации сдвига:
 (4.6)
(4.6)