Номограмма для расчета технико-эксплуатационных показателей автомобильного транспорта при перевозке продукции

Номограммой называется графическое изображение функциональной зависимости между несколькими переменными величинами (например, автотранспортными показателями).

Ею пользуются для нахождения численной величины одной из них по заданным значениям других показателей.

Принцип номографии следующий. Допустим, что по заданным показателям, определяющим суточный объем перевозок Q, т и W, т•км, расстояние груженой ездки /ф, км, необходимо найти количество выработанных т•км (рис. 2.13). Тогда на соответствующие точки шкалы А1 (суточный объем перевозок груза, т) и А2 (lгр – расстояние груженой ездки) накладывается линейка, а на пересечении шкалы А3 с линейкой получаем искомую величину – количество выработанных тонно-километров (т•км = W).

Рис. 2.13. Определение искомого показателя

Рассмотрим использование автотранспортной номограммы с помощью конкретных задач.

Задача 2.1. Рассчитайте некоторые технико-эксплуатационные показатели работы автомобиля на маятниковом маршруте при перевозке Q = 500 т груза первого класса. Грузоподъемность автомобиля qа = 5 т. Расстояние перевозки l = 20 км, среднетехническая скорость движения автомобиля Vт = 25 км/ч, время погрузки-разгрузки tп.р = 40 мин, продолжительность рабочего дня Тн = 9 ч.

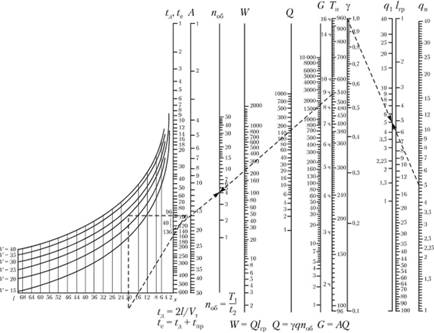
Рис. 2.14. Автотранспортная номограмма:

l – расстояние перевозки, км; Vт – техническая скорость, км/ч; tд – время движения, мин; tпр – время простоя под погрузкой и разгрузкой, мин; tc – время ездки, мин; nоб – количество оборотов, рейсы; Тп – время наряда, ч; γ – коэффициент использования грузоподъемности; Q количество тонн, перевозимых автомобилем; qn – грузоподъемность автомобиля (номинальная); W – количество выработанных т•км; lгр – расстояние груженой ездки; G – объем перевозки, т; А – количество автомобилей; qa – практическая грузоподъемность автомобиля

Решение.

1. Определяем время движения автомобиля за один оборот. К номограмме (рис. 2.14) прикладываем прямоугольный треугольник так, чтобы один его катет был направлен на отметку шкалы расстояния (lгр), а прямой угол коснулся кривой скорости в точке, соответствующей 25 км/ч. Искомый результат будет в месте пересечения второго катета треугольника со шкалой времени и составит 96 мм (рис. 2.15).

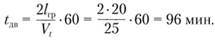
2. Время, затрачиваемое автомобилем за одну ездку (£с), устанавливается так. От отметки 96 мин на шкале времени движения откладывается время (рис. 2.16) простоя под погрузку и разгрузку 40 мин. Получаем 136 мин.

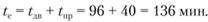
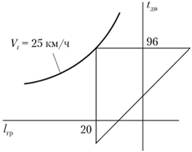
Рис. 2.15. Определение времени движения

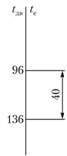
Рис. 2.16. Определение времени оборота

3. Определяем число оборотов автомобиля на маршруте Поб за день работы. Прикладываем линейку таким образом, чтобы она пересекла шкалы lдв – te в точке, соответствующей 136 мин, и шкалу Тн в точке, соответствующей 9 ч (время в наряде). На шкале По6 находим искомую величину – 4,0 (рис. 2.17).

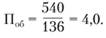
4. Находим фактическую загрузку автомобиля. Накладываем линейку на шкалу γст в точке 1,0 и на шкалу qn в точке 5 (грузоподъемность автомобиля) (рис. 2.18). В точке пересечения линии, соединяющей шкалы γст и qн со шкалой q1 находим результат 5,0 т. В данном случае номинальная грузоподъемность автомобиля и его загрузка совпадают, так как коэффициент использования грузоподъемности для груза первого класса равен единице.

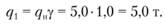
5. Дневная выработка автомобиля в тоннах определяется так (рис. 2.19). Накладываем линейку на шкалу фактической загрузки автомобиля q1 в точке 5,0 и на шкалу Поб в точке 4,0. Результат получается в точке пересечения линии со шкалой Q = 20 т.

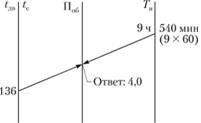
Рис. 2.17. Определение числа оборотов автомобиля

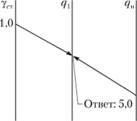
Рис. 2.18. Определение фактической загрузки автомобиля

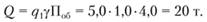
6. Дневная выработка автомобиля в тонно-километрах. Накладываем линейку на шкалу lгр в точке 20 км и на шкалу Q в точке 20. Искомая величина будет лежать на пересечении линии со шкалой W и составит 400 т-км (рис. 2.20).

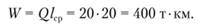
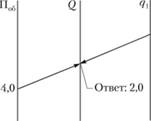
Рис. 2.19. Определение дневной выработки, т

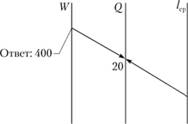
Рис. 2.20. Определение дневной выработки, т•км

7. Определение ходового количества автомобилей для выполнения плана перевозок. Накладываем линейку на шкалу G в точке 500 (заданный объем перевозок) и на шкалу Qдн в точке 20 т. Искомый результат будет получен в точке пересечения линии со шкалой А и равен 25 единицам (рис. 2.21).

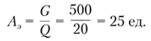
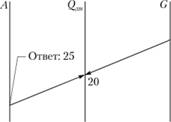
Рис. 2.21. Определение количества автомобилей

Задача 2.2. Определите некоторые показатели при перевозке груза кольцевым маршрутом.

Рис. 2.22. Схема кольцевого маршрута

На рис. 2.22 приведен кольцевой маршрут А – Б – В – Г – А. На участках А – Б и Г – В автомобиль движется с грузом, а Б – В и Г – А – участки холостого пробега. Необходимо организовать работу автомобилей q = 4 т при следующих данных: на участке А – Б протяженностью 15 км перевозится 200 т груза с коэффициентом использования грузоподъемности 0,9, техническая скорость – 30 км/ч, время погрузки и выгрузки – 26 мин. На участке Б – В протяженностью 5 км автомобиль движется без груза со скоростью 35 км/ч. На участке В – Г длиной 20 км перевозится 180 т груза с коэффициентом использования грузоподъемности автомобиля – единица, техническая скорость – 25 км/ч, время простоя под погрузкой и разгрузкой за ездку равно 47 мин. На участке Г – А автомобиль движется без груза со скоростью 20 км/ч. Время в наряде –14 ч.

Решение.

1. Определяем время движения автомобиля на отдельных участках (рис. 2.23), используя часть автотранспортной номограммы, где показано время движения автомобиля (tдв), расстояние перевозки (l) и техническая скорость (VT). Учитывая, что время движения на участке дается для пробега в обоих направлениях, величину, найденную по рисунку, делим на два и получаем искомое время. Например, на участке А – Б время движения (см. рис. 2.22) равно 60 мин (60 : 2), а искомое время составит 30 мин.

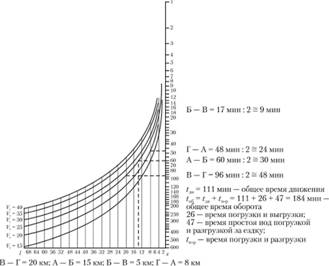
Рис. 2.23. Определение времени движения автомобиля на отдельных участках

Время в наряде определяется по рис. 2.24.

Число оборотов автомобиля на маршруте за время пребывания в наряде находится накладыванием линейки на шкалу tе = 184 и шкалу Тн в точке 14. Искомый результат получится на шкале Zo6 и составит 4,6, округленно 5 оборотов (см. рис. 2.24).

Подсчитаем время, необходимое для совершения 5 оборотов. Линейку накладываем так, чтобы она пересекала на шкале точку te = 184 и Zo6 = 5. Искомый результат на пересечении линии со шкалой Тн. Он равен 920 мин, или 15,3 ч.

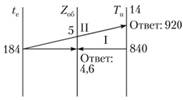
Рис. 2.24. Определение времени в наряде

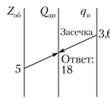
Рис. 2.25. Определение дневной выработки на участке А – Б

Вычислим дневную выработку на участке А – Б (рис. 2.2э). Определяем загрузку автомобиля (qнγ), где qn – грузоподъемность автомобиля – 4 т; γ – коэффициент использования грузоподъемности – 0,9. Поэтому загрузка автомобиля равна 3,6 т (4 0,9). Если автомобиль за день делает 5 оборотов, то дневная выработка составит 18 т. Такая система расчета на участке В – Г, только дневная выработка составит 20 т (рис. 2.26).

Выработка автомобиля в тонно-километрах на участке А – Б (рис. 2.27). Накладываем линейку на шкалу lгр в точке 15 и Qдн в точке 18. Искомая величина будет получена на шкале Wдн в точке пересечения ее с линией – 270 т•км.

Выработка автомобиля в тонно-километрах на участке В – Г. Накладываем линейку на шкалы lгр и Qдн в точке 20. Искомая величина будет получена на шкале Qдн в точке пересечения ее с линией – 400 т•км (см. рис. 2.27).

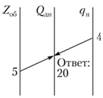
Рис. 2.26. Определение дневной выработки на участке В – Г

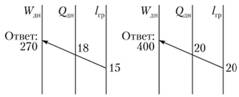
Рис. 2.27. Определение дневной выработки, т•км

Рис. 2.28. Определение эксплуатационного числа автомобилей

Эксплуатационное число автомобилей определяется по участку с наименьшим объемом перевозок, т.е. по участку В – Г. Накладываем линейку на шкалу Qдн, в точках 20 и 180. Искомая величина будет найдена на пересечении линии со шкалой А, и будет равна 9 (рис. 2.28). Следовательно, для выполнения плана перевозок необходимо 9 автомобилей.

Накладываем линейку на шкалу А, в точке 9 и Qдн в точке 18, тогда на шкале (Qпл, линия пересечет точку 162 (см. рис. 2.14).

Таким образом, работа автомобиля на маршруте А – Б – В – Г – А будет рассчитана на перевозку 162 т груза на участке А – Б и 180 т на участке В – Г. Для вывозки 36 т груза на участке А – Б следует организовать маятниковый маршрут с обратным негруженым пробегом и выполнить расчет в последовательности, указанной при решении первого примера.