Модель с фиксированными эффектами против модели со случайными эффектами

В модели со случайными эффектами предполагается, что индивидуальные эффекты не коррелируют с регрессорами. Важно проверить, действительно ли выполняется предположение о такой корреляции, которая может привести к несостоятельности большинства оценок модели со случайными эффектами. Исключение в этом составляют лишь внутригрупповые оценки β-коэффициентов, так как они базируются на преобразовании, которое избавляется от индивидуального эффекта в модели. В результате предположение о том, что они не коррелируют с регрессорами, не связано с несмещенностью и несостоятельностью внутригрупповых оценок.

Дж. Хаусман^[1] в 1978 г. предложил тест, который использует тот факт, что две оценки могут быть определены таким образом, что одна оценка β(1) является состоятельной как при нулевой, так и при альтернативной гипотезе, а вторая оценка β(2) является состоятельной и эффективной, только если справедлива нулевая гипотеза, и несостоятельной – в противном случае. Если полученные оценки β(1) и β(2) принимают достаточно близкие друг к другу значения, то это может свидетельствовать о том, что нулевая гипотеза справедлива. Если полученные оценки β(1) и β(2) отличаются друг от друга, то это может рассматриваться как индикатор того, что нулевая гипотеза не верна. Хаусман показал, что при нулевой гипотезе статистика QH определяемая по формуле

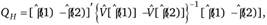(9.74)

где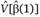и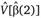– оценки соответствующих матриц ковариаций, является асимптотически распределенной (когда 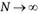) как χ2-распределение со степенью свободы, равной размерности β. Если статистика QH больше, чем квантиль χ2-распределения с соответствующим числом степеней свободы, то мы можем отклонить нулевую гипотезу и принять альтернативную, в противном случае у нас нет оснований для отклонения нулевой гипотезы.

В нашем случае в качестве β(1) мы можем выбрать внутригрупповую оценку 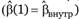, а в качестве β(2) можно выбрать оценкудоступного обобщенного метода наименьших квадратов 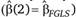. Тогда статистика QH будет иметь вид

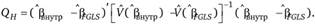(9.75)

Если значение статистики QH больше, чем критическое значение χ2-распределения с kw степенями свободы, где kw – число регрессоров во внутригрупповой модели, то можно отклонить нулевую гипотезу и принять альтернативную, сделав тем самым выбор в пользу модели с фиксированными эффектами. Если же 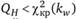, то у нас нет оснований для отклонения нулевой гипотезы и различия между оценками не являются систематическими. Это означает, что можно выбрать модель со случайными эффектами. Получается, что когда внутригрупповая оценка является состоятельной, то оценки доступного обобщенного МНК, обычного МНК и межгрупповая оценка в этом случае не являются состоятельными.

Стоит обратить внимание на то, что этот тест можно провести альтернативным способом. Дж. Хаусман и У. Тейлор (Taylor) в 1981 г. показали, что для вычисления статистики можно также использовать межгрупповую оценку βмеж и оценку доступного обобщенного МНК :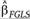

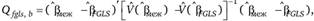(9.76)

или межгрупповую оценку 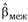и внутригрупповую оценку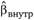

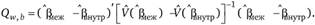(9.77)

Если сравнить полученные значения статистики (9.76) и (9.77) с критическим значением 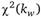, то можно прове

рить ту же самую нулевую гипотезу, что и при помощи статистики (9.75). Все эти три статистики (9.75)–(9.77) на самом деле являются численно идентичными, и можно использовать любую из них.

Таким образом, при помощи теста Хаусмана можно проверить гипотезу об отсутствии корреляции между индивидуальными эффектами и регрессорами и сделать выбор в пользу модели со случайными эффектами либо в пользу модели с фиксированными эффектами.

Для данных нашего примера по индивидуальной заработной плате статистика QH составила 22,09. Критическое значение χ2-статистики для четырех степеней свободы на 5%-ном уровне значимости равняется 9,49. Получается, что 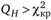, т.е. различия между оценками являются систематическими и индивидуальные регрессоры коррелируют с регрессорами. Таким образом, можно сделать выбор в пользу модели с фиксированными эффектами.