Модель экономики с жесткими ценами

Еще один вариант кейнсианской экономики с жесткими ценами предлагает экономист Б. МакКаллум (McCallum, 1989). Он исходит из базовой негибкости цен на товарных рынках. Предприниматели неохотно идут на изменение цен, поскольку это связано с издержками смены ярлычков (издержки меню), а также с эффектом лояльности покупателей. Чем чаще изменяются цены, тем выше издержки, связанные с необходимостью формирования новых лейблов, ярлычков на все продаваемые товары. И кроме того, фирмы не хотят терять постоянных клиентов.

Функция совокупного спроса может быть получена на основе модели IS–LM.

Линия IS: (рассматриваем случай закрытой экономики).

Линия .

Тогда функция AD будет выглядеть (в логарифмической форме) таким образом^[1]:

где vt – случайная величина, характеризующая стохастический шок спроса;– положительные параметры.

В других обозначениях, операторах ожидания и ценовых логарифмах функция совокупного спроса имеет следующий вид:

Вторая форма нам понадобится для унификации обозначений в модели, где помимо инфляционных встречаются и другие, более сложно формируемые ожидания. Оператор ожидания в этих случаях более уместен, чем простые буквенные обозначения.

Функция совокупного предложения состоит из трех компонентов:

где компонент характеризует рост потенциального ВВП с течением времени (тренд выпуска); компонент демонстрирует явление гистерезиса, запаздывание выпуска; компонент ε, показывает случайную величину – стохастический шок предложения; – положительные параметры.

Основная предпосылка такова: если потенциальный ВВП (выпуск при полной занятости) находится на высоком уровне сегодня, то велика вероятность, что его уровень будет высок и завтра.

Как найти величину ?

Это уровень, соответствующий равновесию на всех рынках в экономике.

Пусть – равновесный уровень цен в экономике. Предположим, что текущий уровень цен есть ожидаемый в прошлом равновесный уровень: . Доминируют рациональные ожидания.

Тогда найдем равновесный выпуск:

Пусть ожидания в отношении динамики ВВП также рациональны:

или

Вместе с тем ожидания равновесного выпуска подчиняются линии совокупного спроса:

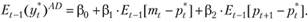
Учитывая, что

никто не может предсказать случайную ошибку и

(наша предпосылка),

приравняем функции (операторы) ожиданий со стороны предложения и со стороны спроса: и выразим искомую величину:

Найдем разницу между фактическим ВВП (линия совокупного спроса) и потенциальным ВВП (линия совокупного предложения при полной занятости):

Или, выполнив арифметические действия, получаем

Каким образом проявляется в данной модели действие монетарных властей?

Пусть центральный банк руководствуется таким монетарным правилом:

где μ0, μ1 – положительные параметры; еt– случайная ошибка, характеризующая монетарные шоки.

Пусть – ожидания монетарных действий следуют тренду монетарных властей. Тогда величина показывает неожиданное изменение предложения денег в предыдущий период (монетарный шок).

Подставим монетарное правило в функцию совокупного предложения:

Мы видим, что систематический и предсказуемый компонент монетарной политики – () – не оказывает никакого воздействия на реальные переменные, так как фирмы учитывают в своих решениях известную им информацию относительно поведения монетарных властей. Реальный эффект на экономику может оказать лишь случайный компонент кредитно-денежной политики, неожиданный монетарный шок.