Методы обработки малых выборок

Разработка новых статистических методов, ориентированных на обработку малого числа наблюдений, была вызвана невозможностью применения традиционных методов математической статистики, которые не подходят для обработки выборок такого объема.

Рассмотрим результаты анализа специальных статистических методов обработки малого числа наблюдений, ограничившись при этом кратким обзором их свойств.

Одними из первых вопрос о назревшей необходимости нового подхода к обработке малых выборок поставили В. В. Чавчанидзе и В. А. Кусишвили, при этом для построения оценки функции распределения они предложили использовать так называемый метод прямоугольных вкладов (МПВ) [29]. Исследования возможностей этого метода привели к разработке серии других методов, основанных на использовании функций вкладов.

Оценки распределений, получаемые вследствие применения этого метода, обобщенно могут быть выражены в виде линейной суммы двух компонент: априорной и эмпирической. При этом эмпирическая компонента строится по данным выборки и представляет собой сумму функций, удовлетворяющих ряду условий:

где f0(x) – априорная компонента; р(х – хi) – составляющая эмпирической компоненты, связанная с i-й реализацией выборки; α0 – вес априорной компоненты.

В основе МПВ лежит использование априорной информации о неизвестном распределении значений параметров изделий и учет случайного характера выборки.

Априорная информация о распределении состоит в следующем: • при известных границах интервала [о; b], для которого определена случайная величинах, плотность распределения удовлетворяет условию

при

при

• плотность распределения непрерывна внутри интервала [a; b] и не имеет очень крутых подъемов и спадов.

Из анализа априорной информации можно заключить, что в качестве априорной компоненты в МПВ целесообразно использовать равномерное распределение, заданное внутри интервала [а; b].

Учет случайного характера выборки выражается в том, что допускается возможность появления любых других значений случайной величины из области , где d – ширина вклада^[1].

Методика построения функции f(x) основывается на использовании в качестве функции вклада единичного прямоугольника, что, собственно, и дало название методу. Плотность распределения записывается в виде

где Ψi(χ) – функция вклада единичной площади.

При этом для некоторых значений xi функция вклада может выходить за пределы интервала [а; b]. В таком случае часть площади, выходящая за границы интервала, отбрасывается, а над оставшимся основанием прямоугольника равномерно надстраивается площадь, равная отброшенной.

В качестве функции вклада могут использоваться также распределения иной формы, например, распределение Симпсона, потенциальная функция (потенциал), дельтообразная функция и др. В известных работах (см., например, [9]) показано следующее:

• для каждого типа распределения существует оптимальная ширина вклада do, при которой эффективность МПВ максимальна; значение do уменьшается с увеличением объема выборки;

• форма вклада оказывает значительное влияние на точность МПВ и простоту реализации;

• оптимальная ширина вклада зависит не только от типа распределения, но и от значений его параметров. При отсутствии таковой информации задача выбора параметров вклада не приводит к определенному решению, поэтому на высокую эффективность МПВ рассчитывать трудно.

Своеобразный подход к определению формы и параметров вклада рассматривается в работе В. И. Шаповалова (УГПУ). Параметры вкладов (ширину, форму и др.) предлагается подбирать таким образом, чтобы из имеющейся выборки извлекалось наибольшее количество информации о функции распределения.

Однако рассматриваемый подход имеет существенные недостатки.

Во-первых, для определения формы вклада используются значения четвертого центрального момента (первый момент – математическое ожидание; второй – дисперсия; третий – эксцесс (несимметрия) ФР; четвертый – куртозис (некрасивость) ФР, т.е. искажения в одну сторону больше, чем в другую).

Во-вторых, для определения оптимальных значений параметров вклада требуется априорное значение типа распределения. Если тип распределения заранее неизвестен, обосновать выбор значений параметров не представляется возможным.

Отметим, что учет случайного характера отдельной реализации набора исходных данных для малой выборки широко используется для анализа больших выборок. При построении гистограммы с каждой реализацией связывается элементарная плотность равномерного распределения на подынтервале, включающем эту реализацию. Суммирование всех элементарных плотностей дает оценку плотности распределения, графическим изображением которой и является гистограмма.

Таким образом, из анализа сущности МПВ и других методов вкладов можно сделать вывод о том, что принципиально новым элементом, обусловливающим высокую эффективность методов при обработке выборок ограниченного объема, является использование априорной информации, заключенной в границах интервала, где определена случайная величина.

И. В. Еременко (УГПУ) и А. Н. Свердлик (УГПУ) предложен эмпирический метод построения функции распределения, названный методом уменьшения неопределенности (МУН). Его отличие от МПВ состоит в том, что вместо ширины прямоугольного вклада d, построенного около реализации хi, используется нормированное равномерное распределение, заданное на интервале [хi-1; xi+1]. Суть МУН заключается в равномерном распределении скачка вероятности в точке .хi.

Выражения для эмпирической функции распределения, получаемой с помощью МУН, можно записать в виде

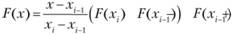
при хi-1 ≤ х < хi и

где ki – число одинаковых значений хi.

Метод уменьшения неопределенности является частным случаем МП В, в котором ширина вклада – случайная величина, изменяющаяся с изменением индекса i.

Метод априорно-эмпирических функций (МАЭФ) разработан И. П. Демаковым (УГПУ) и В. В. Потепуном (УГПУ). В случае использования МАЭФ интегральную функцию распределения можно представить в виде

где Fd(x) – априорное распределение, построенное по априорным данным; Fэ(x) – эмпирическое распределение, построенное по данным выборки; со – коэффициент достоверности информации об априорном распределении.

В основе МАЭФ так же, как и рассмотренных выше методов получения оценок распределений, – использование априорной информации в виде границ интервала [я; b], а также индивидуальный подход к каждой отдельной реализации случайной величины. Однако при этом априорной информации приписывается некоторый вес со и полагается, что

где Δ – интервал дискретности, определяемый точностью наблюдения (измерения) случайной величины.

В известных работах авторов из УГПУ приведены сведения о том, что по эффективности МАЭФ не уступает МПВ, а по простоте реализации подобен МУН. Кроме этого, сильной стороной МАЭФ является то обстоятельство, что значимости априорной информации придается вес, она (значимость) ранжируется с помощью весовых коэффициентов.

Однако отмеченные достоинства на практике можно реализовать лишь тогда, когда имеется достаточно точная информация о предполагаемой функции распределения. В случае отсутствия такой информации МАЭФ вполне может быть отнесен к традиционным методам математической статистики.

Метод сжатия области существования интегральных законов распределения (ИЗР) предложен И. В. Еременко (УГПУ). При использовании этого метода предполагается наличие следующих условий:

• имеется выборка конечного объема, представленная в виде вариационного ряда

• для каждого элемента выборки хi существует единственная последовательность чисел такая, что

• построение оценки распределения состоит в отыскании приближенных значений

(6.1)

Анализ распределения, таким образом, сводится к выбору последовательности, позволяющей минимизировать либо математическое ожидание, либо дисперсию погрешности построения ИЗР для каждого i-го члена вариационного ряда

.

Наиболее предпочтительным при инженерных расчетах является следование алгоритму, основанному на минимизации дисперсии. В этом случае члены ряда (6.1) можно определить следующим образом:

(6.2)

Соединяя полученные значения аi (i = 1,2,..., N) отрезками прямых, получают кусочно-линейную аппроксимацию интегральной функции распределения с узлами в точках {хi, ai}.

Основным достоинством метода сжатия ИЗР является возможность вычисления доверительной вероятности для каждого г-го члена последовательности (6.1). При этом вероятность прохождения ИЗР через заранее выбранный интервал [аi – Δi; аi + Δi] равна

где Ρy,i,N – плотность вероятности прохождения ИЗР на уровне г/(• для г-го испытания в серии из N испытаний.

Эту величину можно описать выражением

Другим достоинством использования метода сжатия ИЗР является обеспечение высокой точности оценивания функции распределения в окрестностях узлов интерполяции.

Недостатком метода сжатия И3Р является то, что точность воспроизведения остальных участков кривой у = F(x) в результате линейной интерполяции при малом числе наблюдений невысока.

Из а нал иза выражения (6.2) можно заключить, что метод сжатия ИЗР является, по сути, частным случаем МПВ. В этом несложно убедиться, если продифференцировать интегральную функцию распределения, получаемую с помощью ИЗР. Вследствие того, что используемые вклады не являются оптимальными, можно утверждать, что по точности метод сжатия ИЗР уступает МПВ.

Г. В. Дружининым и О. В. Вороновой^[2] разработан эмпирический метод построения интегральной функции распределения, названный ими методом последовательных медиан (МПМ). Краткая характеристика этого метода заключается в следующем.

Исходные данные {х1, х2, ..., хN} располагаются в вариационный ряд, находится медиана этого ряда (среднее число в ряду после упорядочения чисел вариационного ряда по убыванию или по возрастанию), и на графике эмпирической функции распределения ставится точка с координатами хш и F(xm) = 0,5. Затем находятся медианы двух половин вариационного ряда и им в соответствие ставятся значения эмпирической функции 0,25 и 0,75 и т.д. Указанная процедура продолжается до тех пор, пока не будут рассмотрены все имеющиеся значения хi (i = 1, 2, ..., N). В результате получается ряд точек Fn(x).

Начальное и конечное значения функции распределения находят по формулам

где х1, х2 – первые два члена вариационного ряда; xi – оценка моды функции распределения (F( xj) = 0,5); при малом числе опытных данных считается, что оценка моды совпадает с оценками медианы по выборке.

Исходя из изложенного материала, можно сделать вывод о том, что МПМ также является одной из разновидностей МПВ. Чтобы в этом убедиться, достаточно продифференцировать получаемую эмпирическую функцию распределения. Весьма интересная особенность МПМ состоит в том, что границы интервала, в котором определена случайная величина, определяются по данным выборки.

Своеобразный подход к построению оценки распределения рассмотрен в работах сотрудников УГПУ Л. Я. Пешеса, М. Д. Степановой, Η. Н. Власовца. Предлагаемый ими метод основан на выдвижении и проверке гипотез, причем в качестве критерия согласия рекомендуется использовать условие совпадения первых трех-четырех моментов распределения. Вид аппроксимирующего распределения определяется в результате оценки попадания расчетных моментов этого распределения в доверительные интервалы для эмпирических моментов. Причем доверительные интервалы для эмпирических моментов определяются при статистическом моделировании эмпирической функции на ЭВМ. Для построения эмпирической функции распределения по выборке некоторыми авторами предлагается использовать МП В (см. [29, т. 2]), причем в качестве функции вклада рекомендуется применять прямоугольник с переменным основаниемι. Функции вклада строятся относительно. При этом интегральную функцию распределения можно записать в виде

(6.3)

где уi – частность i-й реализации случайной величины X.

Алгоритм формирования оценок первых четырех моментов распределения реализуется следующим образом:

• с помощью программного датчика равномерно распределенных случайных чисел вырабатываются случайные последовательности, равномерно распределенные в интервале (0; 1);

• с помощью обратного преобразования получаются случайные последовательности объема N, удовлетворяющие распределению (6.3). С учетом выражения для F(x) значения х определяют по правилу

• по полученным N реализациям случайной величины X оценивают значения первых четырех моментов распределения. Указанные операции повторяют k раз, причем k оценивается с помощью неравенства , где γ – уровень доверия. Величина γ представляет собой вероятность и может быть равна 0,5, 0,7, чаще всего 0,9. Введение уровня доверия в формулу связано с риском исследователя (операциониста в теории операций);

• для каждого из моментов составляют вариационный ряд

где k – момент вариационного ряда ; каждый момент имеет границы в некотором интервале. Границы доверительного интервала определяются величинами, где r1, r2 – целые части чисел

Методика проверки выдвигаемых гипотез заключается в следующем. Для каждого из рассматриваемых теоретических распределений методом максимального правдоподобия определяются значения параметров, после чего вычисляются первые четыре момента, соответствующие этому распределению. Далее выясняется, попадают ли эти моменты в доверительные интервалы для эмпирических моментов. При этом переходят последовательно от более высоких уровней к более низким уровням. В качестве подходящего распределения выбирается такое распределение, моменты которого попадают в самый узкий интервал.

Следует отметить, что авторами данной методики выбран весьма удачный способ идентификации эмпирического и теоретического распределений по значениям начальных моментов, так как совокупность моментов образует минимальную систему достаточных статистик, как следует из теории статистики, однозначно определяющих распределение.

Методика имеет следующие недостатки:

• при малом числе данных значения моментов высших порядков (начиная с третьего) определяются с большой погрешностью;

• оценка распределения (6.3) не является оптимальной вследствие того, что рассматриваемый метод представляет собой одну из разновидностей МПВ, а ширина вклада случайна;

• эффективность метода зависит от анализируемых теоретических распределений. Если в их числе не находится подходящей модели, то перейти к узким доверительным интервалам нс удастся, что является следствием неконструктивного, проверочного характера метода.

Рассмотрим информационный подход к построению оценок распределения по ограниченному числу опытных данных. Количество информации (по Шеннону) о функции распределения, содержащееся в выборке малого объема, ограничено, поэтому оценить распределение по экспериментальным данным можно лишь с определенной степенью точности. Целью разработки новых статистических методов является возможно более полное использование выборочной информации о функции распределения и, следовательно, получение оценок распределений, как можно более близких к истинным (см. 129, т. 2]).

На основе проведенного анализа нетрадиционных методов математической статистики можно заключить, что в случае отсутствия априорных сведений о функции распределения целесообразно строить метод оценивания таким образом, чтобы исключить этапы, требующие использования какой-либо информации, кроме той, которая получена опытным путем. Применение энтропийного подхода позволяет получать оценку распределения на основе лишь экспериментальных данных. В этом случае задача формулируется следующим образом.

Пусть случайная величина X (в общем случае векторная) может принимать ряд значений с вероятностями , которые неизвестны. В результате эксперимента получены средние значения функций

причем m<<n.

Требуется на основе имеющейся информации определить значения вероятностей pi.

Дополнив исходные данные условием нормировки , получим m + 1 уравнение с и неизвестными.

Из постановки задачи очевидно, что однозначно определить значения pi по имеющейся информации не представляется возможным. Поэтому необходим критерий, который из бесконечного множества распределений позволял бы выбрать такое, которое наиболее точно согласуется с имеющимися экспериментальными данными. Опытным путем показано, что в качестве такого критерия следует использовать энтропию распределения. Под энтропией S понимается неопределенность в отношении истинных значений Pi (i = 1, 2, ..., п). Исходная задача при этом сводится к следующей: необходимо определить значения рi доставляющие максимум функционалу

(6.4)

при уравнениях связи

(6.5)

Отметим, что при этом согласно условию задачи тип распределения Ρι полагается неизвестным. При таком подходе из всех распределений, согласующихся с исходными данными и представленных в виде уравнений связи (6.5), необходимо выбрать наиболее

пологое (т.е. наиболее близкое к равномерному) распределение. То есть следует избегать распределений, имеющих острые пики, при которых выделяется тот или иной результат, за исключением случаев, когда того требует условие решаемой задачи.

Таким образом, оценке распределения, полученной на основе энтропийного подхода, соответствует наибольшая неопределенность (согласно (6.4)). Если число возможных значений случайной величины X априорно известно, то количество информации о функции распределения Ijg, извлекаемое в результате обработки исходных статистических данных, определяется соотношением

где S – максимальное значение энтропии распределения (апостериорное); Sапр – исходная неопределенность, соответствующая случаю, когда известно лишь число возможных значений случайной величины, определяемая соотношением

(6.6)

Из анализа выражения (6.6) следует, что оценка, доставляющая максимум неопределенному апостериорному распределению, предохраняет нас от использования любой информации, не связанной с данными выборки.

При использовании информационного подхода предполагается представление всех встречающихся одномерных распределений в единой форме:

где μj – значения параметров распределения, определяемые по значениям vj (например, можно использовать полиномы Лаггера, Чебышева, Эрланга, Якоби, Сонина и др.).

Следует отметить, что выбор характеристик распределения в значительной степени произволен. Например, в качестве центральной точки распределения могут выступать среднее, медиана и мода, в качестве характеристик рассеяния – дисперсия, первый абсолютный момент и широта распределения.

В литературных источниках авторов из УГПУ^[3] показано, что в качестве vj целесообразно использовать значения начальных моментов распределения.

Для этого существует две причины. Первая состоит в том, что поскольку начальные моменты являются усредненными величинами, то при малом числе данных в их значениях обнаруживаются более устойчивые закономерности, чем в самих результатах наблюдений. Вторая причина заключается в том, что совокупность начальных моментов образует минимальную систему достаточных статистик, однозначно характеризует функцию распределения и стохастическую зависимость между переменными, конечно в случае системы случайных величин.

Как это известно из теории математической статистики, для описания практически любого распределения достаточно учитывать только три-четыре начальных момента. Авторами из УГПУ показано, что точность оценок распределения, получаемых с помощью разработанного метода, в целом оказывается выше точности оценок, определяемых с помощью статистических методов аналогичного назначения. Таким образом, для оценки показателей надежности по выборке малого объема целесообразно использовать информационный подход, состоящий из разных методов.