Математические основания для обратных вычислений

Математическим основанием для обратных вычислений является операция дифференцирования функций, где предполагается, что общее приращение функции (результирующего показателя) разлагается на слагаемые. Величина каждого из них определяется как произведение соответствующих частей производной на приращение переменной, по которой вычислена данная производная.

Пусть задана функция 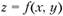. Тогда если функция дифференцируема, ее приращение можно выразить следующим образом:

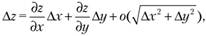
где – прирост функции; – прирост первой переменной (фактора); 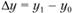– прирост второй переменной (фактора); 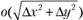– бесконечно малая величина более высокого порядка, чем .

Влияние каждой из переменных на изменение функции z определяется следующим образом:

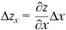и

Для постановки задачи обратных вычислений требуется:

• дополнить прямые зависимости целевой установкой, указав желаемый тренд изменения каждого из аргументов прямой функции;

• указать приоритетность в путях достижения целей, отражаемых с помощью задаваемых коэффициентов.

Детально методы решения такого рода задач представлены в работе [28], здесь же сделаем некоторое их обобщение, связав с теорией факторного анализа. Согласно с данной теорией определить часть прироста функции за счет какого-либо из аргументов можно по формулам из работы [5, с. 98–99]. Например, для мультипликативных моделей эти формулы имеют вид

Тогда, если считать, что желаемые приросты аргументов функции должны быть пропорциональными величине коэффициентов их приоритетности, то данное требование можно записать в виде

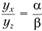, или .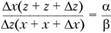

Это позволяет рассчитать те приросты аргументов, которые обеспечат заданный кем-либо прирост функции с помощью системы уравнений, имеющей вид

где 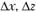– искомые приросты аргументов, зависимые от и коэффициентов приоритетности α, β.

Здесь выражения 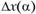и указывают на прирост 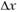от соответствующего коэффициента приоритетности. Обязательным условием выступает ограничение . Очевидно, что 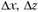можно интерпретировать как управляющие воздействия на соответствующие структурные подразделения предприятия.

Эта же информация может быть представлена графически, где указывается то, что приросты для х и z зависят не только от задаваемого прироста Δу, но и от коэффициентов α и β.

Методы обратных вычислений

Допустим, для прямых расчетов применяется формула, отражающая зависимость рентабельности (Р) от прибыли (П) и себестоимости продукции (С):

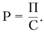
Тогда если у лица, формирующего решение, появилось желание повысить рентабельность за счет повышения прибыли и снижения себестоимости, то такая целевая установка в формуле отразится следующим образом:

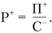
Однако это еще не все. Если известны пропорции, какой части прироста рентабельности желательно добиться за счет повышения прибыли, какой – за счет снижения себестоимости, то пропорции этих частей указываются с помощью коэффициентов приоритетности. Например, если 0,8 прироста рентабельности следует добиться за счет увеличения прибыли, а 0,2 – за счет снижения себестоимости, то тогда формула приобретает вид

где α, β – коэффициенты приоритетности целей (рис. 2.2).

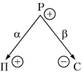
Рис. 2.2. Повышение рентабельности

Целевые установки лица, формирующего решение, могут быть и другими. В этом же примере можно значение Р повысить за счет уже повышения П и С одновременно. Причем приоритетность в достижении подцелей может меняться, а может и нет. Тогда получим следующее аналитическое выражение:

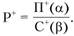
Необходимо заметить, что корректный расчет абсолютных величин приростов далеко не всегда возможен, поэтому в уже упомянутых работах [17, 28, 30] разработано несколько методов, обеспечивающих обработку большинства возможных вариантов прямых зависимостей. Перечислим их:

1) решение задач с помощью индивидуальных коэффициентов прироста аргументов;

2) решение задач с помощью единого коэффициента прироста аргументов;

3) решение задач без коэффициентов прироста аргументов;

4) решение задач без указания приоритетности целей.

Сделаем некоторые замечания.

В простейших случаях, при наличии аддитивной функции и при положительном знаке желаемого прироста функции, а также приростов аргументов, задача решается просто. Для определения неизвестных приростов аргументов достаточно задаваемый прирост функции распределить пропорционально коэффициентам приоритетности целей. Допустим, известна Вперед целевая установка, заданная аддитивной функцией вида 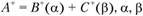– коэффициенты приоритетности целей. Известен также задаваемый прирост функции, равный ΔА, который следует получить в результате увеличения обоих аргументов.

Для решения задачи можно записать следующее:

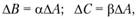
откуда получим

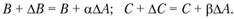
Пример 1. Пусть

Тогда

Проверим результат:

Однако возникает вопрос: как определить приросты для функций, если, во-первых, функции не являются аддитивными, а во- вторых, приросты аргументов имеют различные знаки? Проверим, что получится, если имеется Вперед целевая установка: 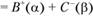. Пусть даны те же значения, что и в примере 1. Если пойти тем же путем, то получим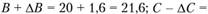

Не будет правильного ответа ни при кратных (дроби), ни при мультипликативных (произведения), ни при степенных и прочих функциях. Нужны обратные вычисления, методы которых излагаются ниже.