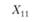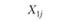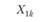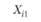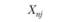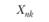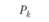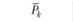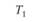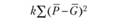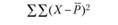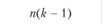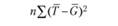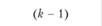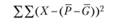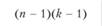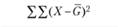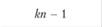Лекция 4. МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПЛАНИРОВАНИИ И АНАЛИЗЕ ЭКСПЕРИМЕНТОВ С ПОВТОРНЫМИ ИЗМЕРЕНИЯМИ
В результате изучения данной главы студент должен:
знать
• особенности планов с повторными измерениями с точки зрения их статистического моделирования;
• структурные предположения, лежащие в основе однофакторного дисперсионного анализа с повторными измерениями для двухуровневых и многоуровневых планов;
• способы применения стандартных процедур однофакторного дисперсионного анализа для связных выборок при обработке экспериментальных данных;
уметь
• правильно планировать внутрисубъектные эксперименты на основе структурных моделей однофакторного дисперсионного анализа для связных выборок и выбирать адекватную им модель статистической обработки;
• правильно интерпретировать основные результаты однофакторного дисперсионного анализа с повторными измерениями и формулировать на их основе адекватные статистические выводы;
• оценивать однородность вариационно-ковариационной матрицы и применять необходимые процедуры в случае неоднородности этой матрицы;
владеть
• базовым теоретико-методологическим аппаратом однофакторного дисперсионного анализа для связных выборок;
• приемами статистической обработки данных методом однофакторного дисперсионного анализа для связных выборок вручную и с помощью статистических программ.
Планы с повторными измерениями
Довольно часто в психологических экспериментах ради экономии сил и времени, а иногда и просто по необходимости приходится использовать одного и того же испытуемого в различных экспериментальных условиях. Таким образом, в отличие от межгруппового плана внутрисубъектный экспериментальный план предполагает использование лишь одной группы испытуемых. Иными словами, результат одного испытуемого в таких экспериментальных условиях характеризует эффекты независимой переменной на различных экспериментальных уровнях.
Внутрисубъектным, или внутригрупповым, называют экспериментальный план, в котором каждому испытуемому предъявляют все без исключения уровни независимой переменной. Эксперимент, реализующий такую схему, принято называть экспериментом с повторными измерениями – ведь в ходе такого эксперимента измерение зависимой переменной у одного и того же испытуемого осуществляется более одного раза. Логика такого экспериментального плана представлена в табл. 4.1.
Таблица 4.1
Однофакторный экспериментальный план с повторными измерениями
|
Испытуемый |
1 |
Условие j |
k |
Сумма |
Среднее |
||
|
1 |
|
… |
|
… |
|
|
|
|
i |
|
… |
|
… |
|
|
|
|
n |
|
… |
|
… |
|
|
|
|
Сумма |
|
… |
|
… |
|
|
|
|
Среднее |
|
… |
|
… |
|
|
Поскольку значения Хij не являются статистически независимыми для разных экспериментальных условий, то для анализа результатов такого рода экспериментов, строго говоря, нельзя использовать модель однофакторного дисперсионного анализа, рассмотренную в гл. 3. Это связано с возможным риском переоценки дисперсии, отражающей влияние экспериментальной ошибки, источниками которой могут стать как внешние факторы, характеризующие влияние собственно экспериментальных условий, так и факторы внутреннего плана, касающиеся самого испытуемого. Понятно, что эти же факторы действуют и в традиционных экспериментальных планах без повторных измерений. Но в них выделить эти два источника дисперсии ошибки не представляется возможным. Другое дело – планы с повторными измерениями.
Дело в том, что в структуре таких экспериментальных планов можно выделить несколько другие части общей дисперсии зависимой переменной, чем те, которые мы уже знаем, а именно: 1) различия между испытуемыми, участвующими в эксперименте, и 2) различия между экспериментальными условиями, которые определяются фактором независимой переменной. Если рассмотрим структуру плана с повторными измерениями, отраженную в табл. 4.1, то можно отметить, что первый источник дисперсии отражает вариацию данных по строкам, а второй – по столбцам. В свою очередь, различия между экспериментальными условиями могут быть вызваны, с одной стороны, эффектом независимой переменной, с другой – внутрисубъектными вариациями, которые могут быть извлечены из совокупной дисперсии экспериментальной ошибки, и потому их принято называть остаточной дисперсией. Наглядной иллюстрацией рассуждений подобного плана может служить рис. 4.1.
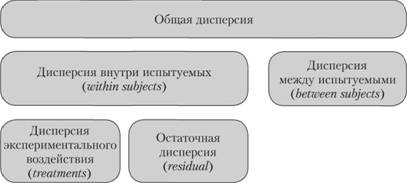
Рис. 4.1. Логика однофакторного дисперсионного анализа с повторными измерениями
Практическая реализация однофакторного дисперсионного анализа с повторным измерением предполагает оценку каждой из составляющих общей дисперсии, представленных на рис. 4.1. Структура данного анализа приведена в табл. 4.2.
Дисперсия данных, вызванная различиями между испытуемыми, очевидно, может быть оценена следующим образом: 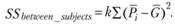
Таблица 4.2
Однофакторный дисперсионный анализ с повторным измерением
|
Источник дисперсии |
Суммарный квадрат (SS) |
Степень свободы (df) |
|
Между испытуемыми |
|
|
|
Внутри испытуемых |
|
|
|
Экспериментальное воздействие |
|
|
|
Остаток |
|
|
|
Общий |
|
|
Дисперсия между экспериментальными условиями, иначе называемая внутрисубъектной дисперсией, очевидно, должна быть оценена так:
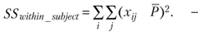 (4.1)
(4.1)
Формула (4.1) тождественна соотношению (4.2), описывающему внутрисубъектную дисперсию как сумму дисперсии, вызванной эффектами независимой переменной (treatment) и остаточной дисперсии (residual):
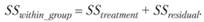 (4.2)
(4.2)
Вариация, вызванная эффектами независимой переменной, в данном случае описывается точно так же, как и в обычной модели дисперсионного анализа, т.е. по формуле (3.2):
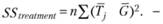
Остаточная дисперсия может быть подсчитана но следующей формуле:
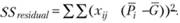 (4.3)
(4.3)
Наконец, общая дисперсия может быть оценена уже известным нам способом, т.е. по формуле (3.3):
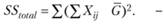
Тот же результат мы получим, если просто просуммируем результаты, отражающие оценку каждого компонента дисперсии, т.е.
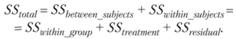
Таким образом, очевидно, что дисперсионный анализ планов с повторными измерениями предполагает разложение общей дисперсии на три аддитивных, т.е. статистически независимых, составляющих: 1) дисперсию, вызванную различиями между испытуемыми; 2) дисперсию, вызванную эффектом независимой переменной; 3) остаточную дисперсию. Дисперсия, вызванная различиями между испытуемыми, имеет п – 1 степеней свободы. Дисперсия, вызванная эффектом экспериментальной переменной, имеет k – 1 степеней свободы. Наконец, остаточная дисперсия имеет (п – 1)(k – 1) степеней свободы. Разделив значения суммарных квадратов на соответствующее им число степеней свободы, можно установить значение средних квадратов для каждого из источников дисперсии. Обычно в подобных экспериментальных планах экспериментатора не интересуют различия между испытуемыми, если, конечно, задача такой оценки нс представляет самостоятельного интереса для исследователя, занимающегося, скажем, изучением фактора индивидуальных различий. Поэтому, как правило, особой нужды вычислять дисперсию, вызванную различиями между испытуемыми, не существует. Таким образом, в итоге проведенных вычислений остаются значения средних квадратов, связанные с эффектами независимой переменной (экспериментального воздействия) и неконтролируемыми вариациями, вызванными индивидуальными особенностями испытуемых, т.е. величины MStreatment и MSresiduat. Величина остаточной дисперсии MSresidual принимается за меру экспериментальной ошибки. Следовательно, для того, чтобы оценить статистический эффект экспериментального воздействия в планах с повторным измерением, достаточно по формуле (4.4) выполнить сравнение дисперсии, вызванной экспериментальным воздействием, с остаточной дисперсией в результате вычисления F-статистики и ее последующего статистического анализа:
 (4.4)
(4.4)
Полученное значение можно оценить с помощью стандартных таблиц F-распределения (см. приложение 4). Но чтобы полученная статистика, действительно, описывалась законом F-распределения, необходимо выполнение некоторых условий, заданных в структурной модели однофакторного дисперсионного анализа с повторными измерениями.