Конические зубчатые передачи

Общие сведения. Комические зубчатые передачи используются для передачи вращения между валами с пересекающимися осями. Назначение конических зубчатых передач – изменить межосевой угол расположения валов, что может сочетаться с изменением угловых скоростей и моментов. Межосевой угол ∑ обычно равен 90° (рис. 4.34). Такие передачи называются ортогональными. Реже используются передачи с другими углами (10° < ∑ < 180°) из-за сложности изготовления корпусных деталей. КПД конических и цилиндрических передач примерно одинаков и равен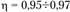

Достоинства конических зубчатых передач аналогичны цили ндрически м.

Недостатки: сложность в изготовлении (нужно выдерживать допуски на углы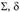) и монтаже из-за необходимости точной фиксации осевого положения (нужно обеспечить совпадение вершин конусов, что требует регулировки положения колес вдоль осей): для изготовления конических колес требуются специальные сложные станки; бо́льшая масса и габаритные размеры, чем у цилиндрических передач; высокая стоимость; наличие осевых сил. Учитывая сложность изготовления, сборки и высокую стоимость, конические передачи нецелесообразно использовать для изменения частоты вращения (обычно нс более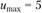), а следует применять лишь для изменения положения валов (межосевого угла).

Кинематика и геометрия конической передачи. Передаточное отношение для конической ортогональной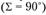 передачи (см. рис. 4.34)

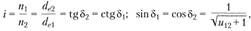(4.44)

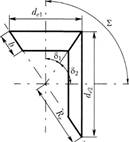
Рис. 4.34

Рис. 4.35

где 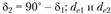– внешние диаметры делительной окружности шестерни и колеса; 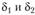– углы делительного конуса шестерни и колеса.

Наиболее распространены конические зубчатые передачи с прямым (рис. 4.35, а) и круговым зубом (рис. 4.35, б). Последние обычно используются при окружной скорости более 3 м/с. В конических передачах вместо начальных и делительных цилиндров их функции выполняют начальные и делительные конусы. На рис. 4.34 приведена схема конической передачи, а на рис. 4.36 – прямозубое коническое колесо, где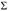– межосевой угол;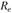– внешнее конусное расстояние;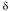– угол делительного конуса;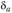– угол конуса вершин;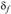– угол конуса впадин.

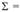
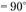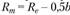Рассмотрим геометрические параметры передачи с и коэффициентом смещения Среднее конусное расстояние используется в расчетах прочности: ; ширина зубчатого венца 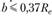; высота ножки, головки и полная высота зуба во внешнем торцевом сечении соответственно

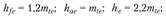
угол ножки (головки) зуба

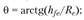
углы конусов вершин и впадин

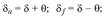(4.45)

внешний и средний диаметры делительной окружности

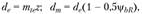(4.46)

где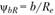– относительная ширина зубчатого венца; внешний диаметр вершин зубьев

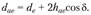(4.47)

Основные размеры, имеющие индекс е, задают на внешнем торце конических колес, где их удобно измерить. Они

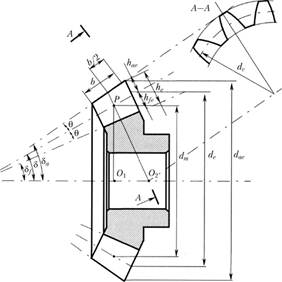
Рис. 4.36

называются внешними. Для конических колес с прямым зубом принимается стандартное значение внешнего окружного модуля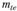, а для круговых – нормальный модуль в среднем сечении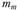на середине ширины зуба. Соотношение между ними следующее:

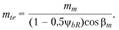
У круговых зубьев преимущественно используют угол наклона зуба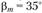на среднем диаметре (см. рис. 4.35, б).

В прямозубых конических передачах зубья понижаются и сужаются от торца к центру. Вершины делительного и внутреннего конусов совпадают. У колес с круговыми зубьями ширина внутреннего конуса имеет такое положение, что ширина дна постоянна, а толщина зуба по делительному конусу увеличивается с удалением от вершины. Эта форма более технологична, так как инструмент обрабатывает сразу весь профиль зуба. В этом случае вершины конусов впадин и вершины делительных конусов не совпадают.

Минимальное число зубьев конической шестернге, принимают при твердости рабочей поверхности более 45 Н RC , – 12-И7; при твердости рабочей поверхности от 350 НВ до 45IIRC3 – 16-Ξ-22; при твердости рабочей поверхности 350 Н В – 19^-27 (большее значение при и = 1, а меньшее при и = 5). С увеличением de число зубьев также увеличивают. Суммарное число зубьев двух колес z = 20-И00.

Из треугольника 0,Р02 (см. рис. 4.36) определим для конических прямозубых передач параметры эквивалентных прямозубых цилиндрических колес:

Рис. 4.37

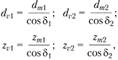(4.48)

где 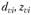– диаметр делительной окружности и число зубьев эквивалентного колеса.

Силы, действующие на конические колеса. Силы от прямозубого конического колеса, действующие на вал, приложены одна (радиальная) перпендикулярно оси, а другая (осевая) параллельно оси, которая нагружает вал изгибающим моментом (рис. 4.37). На конические колеса прямозубой конической передачи действуют силы:

• окружная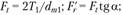

• составляющие силы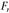

осевая ;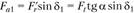

радиальная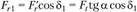

Из рис. 4.37 очевидно, что при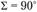

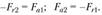
Порядок расчета прямозубой конической передачи на прочность

При проектировочном расчете из условия контактной прочности зубьев определяют приближенное значение внешнего конусного расстояния для прямозубой передачи

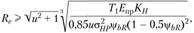(4.49)

где 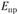– приведенный модуль упругости материала колес.

Значения коэффициента нагрузки 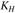и допускаемых контактных напряжений 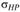определяют аналогично цилиндрическим зубчатым передачам.

Торцевой модуль при определяют по формуле 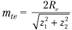и округляют его до величины 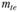по ГОСТу (см. табл. 4.11).

После уточнения модуля вычисляют 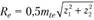, а затем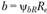.. Геометрические параметры прямозубой конической передачи находят по формулам (4.44)-(4.48) и проводят проверочные расчеты зубьев на контактную и изгиб- ную прочность.

Проверочный расчет на контактную прочность. После условной замены конических колес на эквивалентные цилиндрические с геометрическими характеристиками в среднем сечении определяют расчетные контактные напряжения

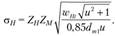(4.50)

Коэффициент 0,85 получен экспериментально при сравнении нагрузочной способности конических и цилиндрических колес. Параметры и 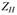определяют по тем же зависимостям, что и для цилиндрических колес.

Удельная окружная нагрузка при расчете контактных напряжений аналогична (4.16):

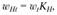
где 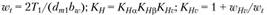– коэффициент, учитывающий дополнительную динамичекую нагрузку 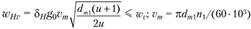окружная скорость в среднем сечении, м/с. Условие контактной прочности зубьев

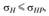(4.51)

где 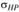– допускаемые контактные напряжения (находятся так же, как и для цилиндрических зубчатых передач).

Проверочный расчет на изгибную прочность. Его проводят для обоих зубчатых колес. Изгибные напряжения для прямозубой шестерни 1 и колеса 2 при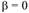

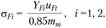(4.52)

Удельная окружная нагрузка при расчетах зуба на изгиб аналогична (4.19):

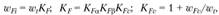
Где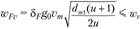

Параметры 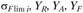рассчитывают так же, как для цилиндрической зубчатой передачи, причем при определении YF берут число зубьев эквивалентного колеса по формуле (4.48); значения параметров 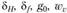выбирают из табл. 4.6, 4.7. Допускаемые напряжени́я при изгибе

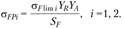(4.53)

Условие изгибной прочности для шестерни 1 и колеса 2

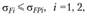(4.54)

где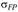– допускаемые напряжения при расчете изгибной прочности зубьев.

Конструкции редуктора. Редуктор с конической передачей приведен на рис. 4.38, где предусмотрена осевая регулировка обоих колес 2 и в. Она обеспечивается изменением толщины регулировочной шайбы 3 и с помощью двух винтов 1. В результате регулировки обеспечивается точная фиксация осевого положения зубчатых колес. Вал 5 закреплен на двух опорах, а шестерня 2 установлена консолъно на вале 4.

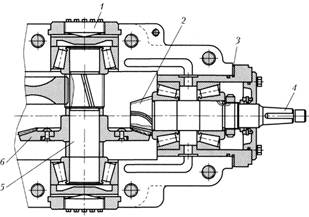
Рис. 4.38