Инициирование горения в холодном газе нагретыми телами

Нагревающееся при эксплуатации оборудование, используемое во взрывоопасных помещениях, способно стать источником инициирования горения. Однако гораздо чаще возможно инициирование не по механизму самовоспламенения – внутри нагретого реактора, а в другом режиме – при контакте холодного в большей части газа с нагретой поверхностью. Условия возникновения прогрессивного само- разогрева здесь существенно иные. Процесс инициирования очага горения нагретым телом в холодной взрывчатой среде мы будем называть поджиганием, в отличие от самовоспламенения в нагретом сосуде.

Для простоты рассмотрим стационарное распределение температуры во взрывчатой газовой среде вблизи бесконечной плоскости, где температура равна Тп вдоль нормальной к плоскости координаты х (рис. 5.12). Теплота реакции может отводиться из зоны, примыкающей к поджигающей поверхности, в бесконечное пространство, заполненное взрывчатой средой с температурой T0, распределение температуры описывает кривая 1. Очевидно, что условия теплоотвода из зоны реакции здесь гораздо благоприятнее, чем при самовоспламенении внутри нагретого сосуда, где тепло могло отводиться только в его стенки. Поэтому переход к нестационарному тепловому режиму в нагретом сосуде становится возможным, когда его температура много меньше критической температуры стенки, поджигающей холодный газ. Критическое для перехода от стационарного теплового режима к нестационарному значение Тr мы будем называть температурой поджигания Ts.

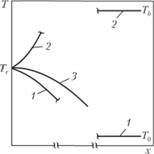
Рис. 5.12. Распределение температуры во взрывчатой газовой среде вблизи бесконечной нагретой поверхности:

1 – Tr < Тs, стационарный режим; 2 – Tr > Тs, прогрессивный саморазогрев; 3 – Тr= Тs, предел поджигания

Основные закономерности для пределов поджигания в отсутствие каталитической реакции на стенке сформулированы Я. Б. Зельдовичем^[1]. Уравнение теплопроводности в этой задаче отличается от соответствующего уравнения для дефлаграции отсутствием конвективного слагаемого, поскольку газ неподвижен. Для стационарного режима при λ = const

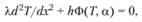(5.12)

где λ – теплопроводность; h – высота реактора; Ф – скорость реакции; а – коэффициент теплообмена.

Вследствие интенсивного теплоотвода температура газа быстро, как и в пламени, понижается от Тr до Т0. Поэтому в пределах узкой зоны реакции конвективные потоки пренебрежимо малы. Можно не учитывать и форму поджигающей поверхности, если ее радиус кривизны велик но сравнению с параметром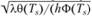(Θ – характеристический интервал температуры). Последний приблизительно равен ширине фронта пламени, у которого Тb = Ts.

Было показано, что для предельного режима перехода от стационарной медленной реакции (кривая 1 на рис. 5.12) к нестационарной (кривая 2) градиент температуры равен нулю (кривая 3). При этом реакция у поверхности настолько интенсивна, что теплоотвод от стенки к газу прекращается. Величина Ts входит в граничное условие уравнения

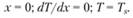(5.13)

Обозначим 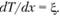Тогда

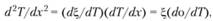(5.14)

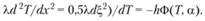
В пристеночной зоне кондуктивного теплоотвода, для которой справедливы уравнения (5.13) и (5.14), тепловой поток от стенки q возрастает при удалении от поверхности (от нуля при Tr = Тs). При этом он быстро достигает постоянного значения, соответствующего Ф = 0, вследствие экспоненциального характера зависимости Ф(Т). При дальнейшем понижении температуры q снова уменьшается до пуля (ветви кривых 1 и 2 па рис. 5.12: Т(х) = Т0 и Т(х) = Тb). Однако для вычисления пределов эти области уже не существенны. Предельное значение qкр можно определить, интегрируя уравнение (5.14), основываясь на сделанных предположениях. Распространяя границу интегрирования до Т= Т0 (поскольку Ф мало), запишем:

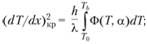(5.15)

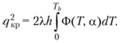(5.16)

Если пренебречь изменением концентрации у поверхности при выгорании, интегрирование (5.16) дает

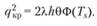(5.17)

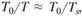
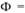
В работе Д. Миллера и др .^[2] решение (5.17) было уточнено с учетом изменения концентрации недостающего компонента при подобии полей концентрации и температуры, которое с известными отличиями справедливо и для данной задачи. Поскольку Ф мало за пределами сравнительно узкого температурного интервала, для учета термического расширения можно приближенно принять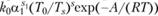, где /io – прсдэкспонента константы скорости; s – порядок реакции. Преобразуя экспоненту, находим:

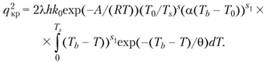(5.18)

Для s1 = 1 находим после ряда приближенных преобразований:

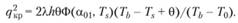(5.19)

Уточненное решение отличается от приближенного (5.17) па множитель (Тb – Ts + θ)/(Тb – Т0).