Двунаправленная модель панельных данных с фиксированными эффектами

Двунаправленная модель с фиксированными эффектами помимо индивидуальных эффектов αi, включает также временные эффекты γt:

(9.78)

где

Эту модель можно оценить путем добавления (Т – 1) фиктивных переменных для соответствующих периодов времени наряду c (N-1) фиктивными переменными, которые соответствуют различным объектам наблюдения. Однако если N или Т являются большими, то в регрессии будет слишком много фиктивных переменных QV + Т – 2), что приведет к огромной потере в степенях свободы и к необходимости обратить большую матрицу размерностью (N + T + K-1). Другой способ получения оценок β-коэффициентов в модели (9.78) заключается в использовании внутригруппового преобразования, предложенного в 1969 г. Т. Уолласем и Э. Хусейном^[1], которое исключает из модели эффекты а, и у(:

(9.79)

где

Преобразования и приведут соответственно к следующим значениям и :

где

где

Построим регрессию на :

(9.80)

Оценивание методом наименьших квадратов уравнения регрессии (9.80) дает внутригрупповую оценку для двунаправленной модели 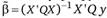. Оценка константы может быть найдена как разница между и . Внутригрупповые оценки эффектов αi и yt будут иметь вид

(9.81)

Результаты оценивания модели (9.80) методом наименьших квадратов представлены в табл. 9.4.

Таблица 9.4. МНК-оценки уравнения регрессии (9.80)

Переменные	ЕХР	ЕХР_2	RUS	UNSKILL
Коэффициенты	0,1439	-0,0008	0,1220	-0,1411
Стандартные ошибки	(0,1484)	(0,0003)	(0,0388)	(0,0828)

Следует обратить внимание на то, что внутригрупповая оценка не позволяет оценить постоянные во времени эффекты, а также переменные, не изменяющиеся по индивидам, потому что Q-преобразование исключает из уравнения все эти переменные. Если истинной моделью является двунаправленная модель с фиксированными эффектами, то оценивание методом наименьших квадратов объединенной модели принесет смещенные и несостоятельные оценки коэффициентов регрессии, так как объединенная модель не включает оба множества фиктивных переменных, тогда как оценки однонаправленных фиксированных эффектов игнорируют только временные фиктивные переменные. Если же эти временные фиктивные переменные являются статистически значимыми, то это будет приводить к смещению оценок однонаправленных фиксированных эффектов из-за пропущенных переменных в модели.

Для того чтобы определить, присутствуют ли в модели индивидуальные и временные эффекты одновременно или по отдельности, можно проверить следующие гипотезы.

Гипотеза об отсутствии индивидуальных и временных эффектов

Гипотеза

гипотеза H1: не H0.

Для проверки нулевой гипотезы вычисляется F-критерий

(9.83)

где SS – сумма квадратов остатков в модели без ограничений

– сумма квадратов остатков в объединенной модели

В случае если вычисленное значение F-критерия окажется больше критического значения для соответствующих степеней свободы и уровня значимости, то мы можем отклонить нулевую гипотезу и принять альтернативную, в противном же случае у нас не будет оснований для того чтобы отвергнуть нулевую гипотезу.

В нашем примере суммы квадратов остатков в модели без ограничений и в объединенной модели будут соответственно равны и. Тогда при критическом значении F-критерия на 5%-ном уровне значимости 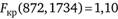. Так как , то мы можем отклонить нулевую гипотезу об отсутствии индивидуальных и временных эффектов и принять альтернативную гипотезу. Мы можем сделать вывод о том, что индивидуальные эффекты и временные эффекты являются совместно статистически значимыми на 5%-ном уровне значимости.