Доходность облигаций

Практика формирования инвестиционных портфелей международных компаний свидетельствует, что инвесторам для оптимизации портфеля зачастую недостаточно информации о рыночных ценах на облигации. Так, при отборе в оптимальный инвестиционный портфель конкретных облигаций им необходимо оценивать финансовую эффективность своих решений, что практически невозможно сделать, не рассчитав доходность ценных бумаг, отбираемых в инвестиционный портфель. Расчет доходности облигации, или так называемой инвестиционной нормы, которую облигация будет обеспечивать, когда будет куплена за данную цену, остается, возможно, наиболее важной задачей, касающейся облигаций. Только решив ее, инвестор может определить, какая из нескольких облигаций обеспечит ему наилучшую инвестицию.

В самом общем случае под доходностью любой инвестиции понимается процентная ставка, позволяющая уравнять приведенную стоимость денежных потоков конкретной инвестиции с ценой (стоимостью) инвестиции.

В случае инвестиций в облигации доходность облигаций – это процентная ставка г, удовлетворяющая следующим уравнениям:

1) бескупонные облигации:

Определение доходности бескупонной облигации

Доходность бескупонной облигации – это, в соответствии с вышесказанным, годовая ставка процента, получаемая инвестором, купившим и владеющим данной облигацией до момента ее погашения.

Для определения доходности по бескупонным облигациям, срок погашения которых превышает один год, следует использовать формулу приведенной стоимости облигации

Пример. Рассмотрим бескупонную облигацию со сроком погашения 2 года (n = 2), номинальная стоимость которой 1000 долл. США, а покупная цена 880 долл. Требуемая доходность – 8% годовых.

Ее доходность составит

2) облигации с купонными выплатами:

откуда

Расчет свидетельствует о нецелесообразности приобретения инвестором рассматриваемой облигации.

Определение доходности по купонной облигации

Для купонной облигации в отличие от бескупонной различают текущую доходность и внутреннюю ставку дохода, или доходность к погашению.

Текущая доходность расчитывается по формуле

где – текущая доходность; С – купонный доход по облигации (купон); Р – текущая цена облигации.

Примечание. Здесь используется именно текущая цена, а не та цена, которая была уплачена за облигацию инвестором.

При вычислении текущей доходности в расчет принимаются только купонные выплаты. Другие другие источники дохода, поступающего владельцу облигации, не рассматриваются. Не учитывается, например, прирост капитала, получаемый инвестором, приобретающим облигацию с дисконтом и держащим ее до погашения; в то же время не рассматривается и убыток, который терпит инвестор в случае, если он додержал до погашения облигацию, купленную с премией. Временна́я стоимость денежных средств здесь также не принимается в расчет.

Следовательно, текущая доходность представляет собой, образно говоря, фотографию доходности на данный момент времени, которая в следующий момент может измениться в соответствии с изменениями рыночной цены облигации. Показателем текущей доходности целесообразно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет испытывать существенные колебания.

Более объективный показатель доходности – доходность к погашению, или внутренняя доходность, так как при ее вычислении учитывается не только купонный доход и цена облигации, но также и период времени, который остается до погашения. Внутреннюю доходность можно рассчитывать по формуле оценки рыночной цены облигации

Облигации служат предметом оживленной торговли, поэтому участникам фондового рынка известны не только номинальная стоимость и купонная ставка процента, но и рыночная цена каждой ценной бумаги. Если считать, что рынок характеризуется состоянием совершенной конкуренции, можно считать, что цена облигации равна ее приведенной стоимости.

Таким образом, покупателю облигации известны вес параметры уравнения цены облигации, кроме ставки дисконтирования r. Следовательно, формулу приведенной стоимости можно использовать для того, чтобы на основании рыночной информации вычислить значение ставки дисконтирования, или внутренней доходности r.

К сожалению, данное уравнение не решается в конечном виде: исчислить доходность можно только с помощью специальной компьютерной программы. Можно воспользоваться также методом подстановки в формулу цены облигации различных значений внутренней доходности с расчетом соответствующих им цен. Операцию повторяют до тех пор, пока значение рассчитанной цепы не совпадет с заданной ценой облигации (рис. 3.8).

Рис. 3.8. Алгоритм расчета доходности купонной облигации

Иногда для принятия финансового решения достаточно определить только приближенный (ориентировочный) уровень доходности облигации. Кстати, он может быть использован в качестве исходного уровня доходности в первом блоке рассмотренного выше алгоритма.

Традиционно используемая формула расчета приближенного уровня доходности облигации имеет вид

где r – внутренняя доходность (доходность к погашению); N – номинальная стоимость облигации; Р – цена облигации; п – количество лет до погашения; С – купонный доход; – средний годовой доход; – средняя стоимость облигации.

В ряде случаев лучшее приближение дает формула Р. Родригеса

Например, при оценке внутренней доходности облигации с пятилетним сроком обращения и 10%-ной купонной ставкой при номинале 1000 долл. США и текущей цене 1059,12 долл. точное решение составит 8,5%; традиционная формула дает значение 8,56%, а формула Р. Родригеса – 8,48%. Эта формула обеспечивает хорошее приближение при условии невысокого уровня купонной ставки (ниже 50% годовых) и близких значений цены облигации и ее номинальной стоимости.

В частности, если цена отличается от номинала более чем в 2 раза, то применение обеих формул расчета приближенных оценок недопустимо. Следует также отметить, что погрешность расчетов по формулам приближенных оценок тем выше, чем больше лет остается до погашения облигации. Если облигация продается со скидкой, рассматриваемые формулы дают заниженное значение доходности облигации, если с премией, то завышенное.

Умение вычислять внутреннюю доходность облигаций настолько важно, что разработаны специальные компьютерные программы, определяющие значения г для любых сочетаний цены облигации, срока до погашения, купонной ставки процента и номинальной стоимости. В настоящее время выпускаются даже карманные калькуляторы, способные выполнять расчеты такого рода.

Пример. Облигация с купонной ставкой 8% и номиналом 1000 долл. США приобретена за 1050 долл. за четыре года до погашения. Принимая во внимание, что купоны погашаются один раз в год, определите внутреннюю ставку доходности.

Решение.

Воспользуемся формулой для расчета приближенного значения внутренней доходности облигации:

Применив метод подстановки, получаем:

Поскольку 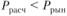(1047,20 с 1050), повторим расчет для скорректированного в меньшую сторону значения г, взяв для этого, например г= 0,0655. В этом случае практически совпадает с рыночной (действительной) ценой облигации, что позволяет закончить расчет показателя внутренней доходности на уровне г = 0,0655, или 6,55%.

Процедура повторных расчетов по методу подстановок может быть значительно ускорена, если имеется график зависимости приведенной стоимости облигации от уровня ее внутренней доходности. Он может быть построен по нескольким точкам, координаты которых (пары значений г и приведенной стоимости) несложно определить по специальным таблицам, приводимым в каждом учебном пособии по финансовым вычислениям. Для рассматриваемого нами примера графическая интерпретация расчета уровня внутренней доходности приведена на рис. 3.9.

Рис. 3.9. Зависимость приведенной стоимости (цены) облигации от уровня се внутренней доходности

Для ускорения процесса расчета внутренней доходности облигации может быть использована также формула линейной интерполяции

где Г[, г2 – значения соответственно заниженного и завышенного уровней ориентировочной доходности облигаций; Р,, Р2 – расчетные рыночные цены облигации, соответствующие уровням доходности Г] и r2; Р – фактическая (действительная) цена облигации на фондовом рынке.

Резюмируя вышесказанное, отметим, что доходность к погашению позволяет оценить не только текущий (купонный) доход, но и размер прибыли или убытка, ожидающих капитал инвестора, остающегося владельцем облигации до ее погашения эмитентом. Кроме того, доходность к погашению принимает в расчет временны́е параметры денежных потоков. Соотношение между уровнями купонной ставки, текущей доходности, а также доходности к погашению представлены в табл. 3.3.

Таблица 3.3

Соотношение основных параметров облигации

Облигация продается	Соотношение между параметрами облигации
По номиналу	Купонная ставка = Текущая доходности = Доходность к погашению
С дисконтом	Купонная ставка < Текущая доходности < Доходность к погашению
С премией	Купонная ставка > Текущая доходности > Доходность к погашению