Диаграммы структуры

Большую группу графиков составляют структурные диаграммы. Это такие диаграммы, в которых отдельные статистические совокупности сопоставляются по их структуре, характеризующейся соотношением разных параметров совокупности или ее отдельных частей.

Широко распространенный метод графического изображения структуры статистических данных заключается в составлении структурных круговых или секторных диаграмм. Секторные диаграммы удобно строить следующим образом: всю величину явления принимают за 100%, рассчитывают доли отдельных частей в процентах. Круг разбивают на секторы пропорционально частям изображаемого целого. Таким образом, на 1% приходится 3,6°. Для получения центральных углов секторов, изображающих доли частей целого, необходимо их процентное выражение умножить на 3,6°. Секторные диаграммы позволяют не только разделить целое па части, но и сгруппировать отдельные части, давая как бы комбинированную группировку долей по двум признакам.

Пример. Рассмотрим построение секторной диаграммы по данным, приведенным в табл. 4.3.

Таблица 4.3/ Данные об охвате населения телевизионным вещанием на конец 2010 г. в N-м регионе

Показатель	Число и	принимаемых грамм
	и более	2	1	0
Удельный вес населения, % к итогу		57.5	1.1	2,1

Построение секторной диаграммы начинается с определения центральных углов секторов.

Для этого процентное выражение отдельных частей совокупности но каждой категории умножим на 3,6°. Три и более телевизионные программы — 131,7°; две — 207°; одна — 14,8°; ни одной — 7,6°. По найденным значениям углов круг делится на соответствующие сектора (рис. 4.11).

Рис. 4.11. Охват населения телевизионным вещанием в N-м регионе на конец 2010 г.

Другим видом структурных статистических диаграмм являются полосовые диаграммы удельных весов, отражающие структуры сравниваемых совокупностей по процентному соотношению в них отдельных частей, выделяемых потому или иному количественному или атрибутивному признаку. Эти диаграммы получены путем преобразования простой полосовой диаграммы с подразделенными полосами. Полосовые диаграммы удельных весов могут вскрыть существенные особенности многих изучаемых экономических явлений.

Пример. Необходимо изобразить графически данные, приведенные в табл. 4.4.

Таблица 4.4/ Данные, характеризующие структуру потребительских расходов населения в N-м регионе за период 2009-2010 гг., %

Показатель	2009 г.	2010 г.
Все потребительские расходы, в том числе:	100	100
продукты питания	1.1	41,7
непродовольственные товары	31	312
алкогольные напитки	2,4	2,2
оплата услуг	17,3	19,9
Изобразим эти данные графически в виде полосовой диаграммы, цель которой — показать изменение удельных весов потребительских расходов населения за два года (рис. 4.12).

Рис. 4.12. Динамика удельного веса потребительских расходов населения в N-м регионе за период 2009—2010 гг.

Значительными преимуществами полосовых структурных диаграмм по сравнению с другими видами являются их большая емкость, возможность отразить на небольшом пространстве большой объем полезной информации. Секторные же диаграммы выглядят убедительно при существенных различиях сравниваемых структур, а при небольших различиях они могут быть недостаточно выразительны.

Диаграммы динамики

Для изображения и внесения суждений о развитии явления во времени строят диаграммы динамики. Для наглядного изображения динамики явлений используют многие диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, радиальные и др. Выбор вида диаграмм зависит в основном от особенностей исходных данных, от цели исследования. Например, если имеется ряд динамики с неравно отстоящими уровнями во времени (1913, 1940, 1950, 1980, 2000, 2010 гг.), то часто для наглядности используют столбиковые, квадратные или круговые диаграммы. Они зрительно впечатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки. Если число уровней в ряду динамики велико, то целесообразно применять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии.

Для построения линейных диаграмм используют систему прямоугольных координат. Обычно но оси абсцисс откладывают время (годы, месяцы и т.д.), а по оси ординат наносят масштабы для отображения явлений или процессов. Особое внимание следует обратить на масштаб осей координат, поскольку от этого зависит общий вид графика. Обеспечение равновесия, пропорциональности между осями координат необходимо в диаграмме, так как нарушение равновесия дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ординат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колебания. Если в ряду динамики данные за некоторые годы отсутствуют, это должно быть учтено при построении графика. Равным периодам времени и размерам уровня должны соответствовать равные отрезки масштабной шкалы.

Пример. Рассмотрим построение линейной диаграммы на основании следующих данных по динамике производства газетной бумаги в регионе за период 2001—2010 гг.:

Год.............2001 2002 2003 2004 2005 2006 2007 2008 2009 2010

Производство,

Млн.т...........237 179 189 158 186 192 172 191 210 211

Изображение динамики производства газетной бумаги на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 ноля диаграммы остается неиспользованным, и это ничего не даст для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикального нуля, т.е. шкала значений разрывается недалеко от нулевой линии, и на диаграмму попадает лишь часть возможного поля графика. Это не приводит к искажениям в изображении динамики изучаемого процесса, и его изменения показываются диаграммой более четко (рис. 4.13).

Рис. 4.13. Динамика производства газетной бумаги в регионе за период 2001-2010 гг.

Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких показателей служит рис. 4.14.

Рис. 4.14. Динамика экспорта и импорта РФ рыбы и ракообразных, моллюсков и других беспозвоночных за 2003-2007 гг.

Линейные диаграммы с равномерной шкалой имеют недостаток, снижающий их познавательную ценность. Этот недостаток заключается в том, что равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателен на протяжении исследуемого периода. Однако при изучении динамики важно знать и относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения.

Именно относительные изменения экономических показателей в динамике искажаются при изображении их на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, которые обычно имеют место в динамических рядах за длительный период времени.

В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему. Полулогарифмической системой называется система, в которой на одной оси нанесен линейный масштаб, а на другой — логарифмический. В данном случае логарифмический масштаб наносят на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (годам, кварталам, месяцам, дням и т.д.). Техника построения логарифмической шкалы Вперед: найти логарифмы исходных чисел; построить ординату и разделить на несколько равных частей. Затем нанести на ординату (или равную ей параллельную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например 0'.000; 0,3010; 0,4771; 0,6021; ...; 1,000, что дает 1, 2,3,4,10. Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате.

Пример. Допустим, нужно изобразить на графике динамику производства угля в регионе за 1980—2010 гг., за эти годы его рост составил 9,1 раза. С этой целью найдем логарифмы для каждого уровня ряда (табл. 4.5).

Найдя минимальное и максимальное значения логарифмов производства угля, построим масштаб с таким расчетом, чтобы все данные разместились на графике. В соответствии с масштабом найдем соответствующие точки, которые соединим прямыми линиями. В результате получим график (рис. 4.15) с использованием логарифмического масштаба на оси ординат.

Таблица 4.5 Динамика производства угля в регионе за период 1980—2010 гг., млн т

Год	Производство К,	1-й V,
1980	170	2,23
1985	292	2,46
	507	2.70
1995	741	2,84
2000	1039	3,02
2005	1294	3,11
2010	1544	3,19

Рис. 4.15. Динамика производства угля в регионе за период 1980-2010 гг.

К диаграммам динамики относятся и радиальные диаграммы, построенные в полярных координатах и предназначенные для отражения процессов, ритмически повторяющихся во времени. Чаще всего эти диаграммы применяют для иллюстрации сезонных колебаний, и в этом отношении они имеют преимущество перед статистическими кривыми. Радиальные диаграммы подразделяют на два вида: замкнутые и спиральные. Эти два вида диаграмм отличаются друг от друга по технике построения; все зависит от того, что взято в качестве базы отсчета — центр круга или окружность.

Замкнутые диаграммы отражают весь внутригодовой цикл динамики одного года. Их построение сводится к следующему: строят круг, среднемесячный показатель приравнивают к радиусу этого круга, затем весь круг делят на 12 равных секторов посредством проведения радиусов, которые изображают в виде топких линий. Каждый радиус изображает месяц, причем расположение месяцев аналогично циферблату часов. На каждом радиусе делают отметку в определенном месте согласно масштабу, исходя из данных на соответствующий месяц. Если данные превышают среднегодовой уровень, то отметку ставят вне окружности па продолжении радиуса. Затем отметки различных месяцев соединяют отрезками.

Пример. Необходимо изобразить с помощью замкнутой диаграммы динамику индексов потребительских цен на все товары и услуги в одном из регионов по месяцам 2010 г. по следующим данным, % к декабрю прошлого года:

Январь..............................................................101,68

Февраль...........................................................102,81

Март.................................................................103,42

Апрель.............................................................104,01

Май...................................................................104,67

Июнь................................................................105,66

Июль................................................................106,58

Август..............................................................106,68

Сентябрь.........................................................107,52

Октябрь...........................................................109,28

Ноябрь.............................................................110,62

Декабрь............................................................111,87

Среднемесячный индекс равен 106,2

Построим круг радиусом, равным среднемесячному показателю. 11а горизонтальном диаметре построим шкалу, взяв длину радиуса, равную 4 см. Следовательно, 1 см = 106,2/4 = 26,6% (рис. 4.16).

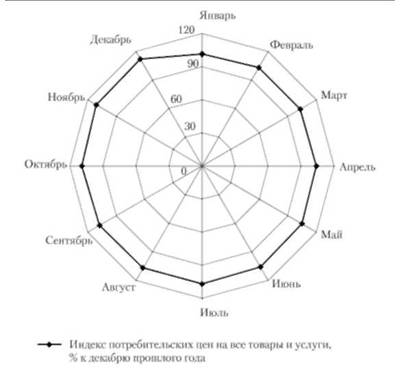
Рис. 4.16. Сезонные колебания индекса потребительских цен на все товары и услуги в регионе за 2010 г., % к декабрю прошлого года

Если в качестве базы отсчета берется окружность, такого рода диаграммы называют спиральными. Спиральные диаграммы отличаются от замкнутых тем, что в них декабрь одного года соединяется не с январем данного же года, а с январем следующего года. Это дает возможность изобразить весь динамический ряд за несколько лет в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом ряд обнаруживает неуклонный рост из года в год.

Для отображения зависимости одного показателя от другого используют диаграмму взаимосвязи. Один показатель принимают за X, а другой за У (т.е. функцию от X), затем строят прямоугольную систему координат с масштабами для показателей, в которой формируется рисунок.

С повышением стоимости основных производственных фондов происходит увеличение затрат на реализацию продукции. Данная зависимость этих показателей может быть выражена линейной связью (рис. 4.17).

Рис. 4.17. Зависимость уровня затрат на реализацию продукции от стоимости основных производственных фондов

Диаграммы взаимосвязи имеют большое значение на практике, так как множество различных показателей связаны между собой либо прямой, либо обратной формой связи. Они могут использоваться также для отображения различных циклических процессов (например, инфляционной спирали), взаимно накладывающихся явлений и т.п.