Деградация изделий как процесс с немонотонными реализациями

В общем случае начальные условия, исходя из искомой функции λ(t0, x0; t, х) (плотности вероятностей) могут быть заданы, например, в виде [31]:

где λ0(x0) – некоторое произвольное распределение исследуемого параметра в начальный момент.

Если начальное значение параметра х задано (можно положить t0=0; x0 0), то λ0(x0) вырождается в δ-функцию:

(4.13)

Для определения граничных условий необходимо оценить характер реализаций процесса x(t). Для ИЭТ здесь имеются в виду реализации, выражающиеся как изменение определяющих параметров невосстанавливаемых объектов. Первое достижение реализацией границы заданной области (в нашем случае параметр изменяется от нуля до единицы) соответствует отказу объекта. По характеру изменения реализации необходимо определить, моделирует ли отказ первое достижение реализацией границы заданной области и может ли реализация повлиять на изучаемый процесс x(t) и соответственно на искомую функцию λ(t, х) в дальнейшем, т.е. после первого достижения границы.

В случае когда реализация имеет немонотонный характер, после первого достижения границы заданной области (что соответствует отказу и снятию изделия с наблюдения) она может снова возвратиться в заданную область и участвовать в наблюдаемом процессе. Для того чтобы первое достижение границы немонотонной реализацией моделировало отказ и в дальнейшем реализация не участвовала в наблюдаемом процессе и, значит, не влияла на λ(t, х), необходимо на границе заданной области поставить граничное условие типа поглощающего экрана. В этом случае любая реализация, впервые достигнув его, навсегда останется на границе, вне заданной области.

Так как рассматриваемые реализации процесса деградации изделий имеют немонотонный характер, в качестве граничных при решении уравнения (4.5) принимаются условия

(4.14)

(4.15)

Граничное условие (4.14) – чисто формальное. Поскольку изучаемый процесс (определяющий параметр изделий) не может принимать отрицательные значения, установленная левая граница является недостижимой (естественной) и никак не влияет на процесс в заданной области. Принятие формального условия (4.14) необходимо для решения уравнения (4.11).

Граничное условие (4.15) вытекает из приведенных соображений и соответствует поглощающему экрану в точке х= 1.

Решение уравнения (4.11) для краевых (граничных) условий (4.13)-(4.15) можно записать в следующем виде [4, 31, 38]^[1]:

(4.16)

В результате дифференцирования равенства (4.16) по времени получается выражение

после подстановки которого в формулу (4.12) и интегрирования получается уравнение плотности распределения времени до первого отказа

Представив последний интеграл в виде суммы интегралов, авторы [31] получают компактное выражение для плотности распределения времени до первого отказа:

где

Для определения первого интеграла Ji делается подстановка

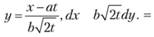
При

при

. Тогда

Произведя обратную замену переменных, авторы [31] получают

Выполнив необходимые преобразования (подстановки и замену переменных), авторы [31] получили результат интегрирования и для J2:

После суммирования J1 и J2 и сокращения на 2 числителя и знаменателя выражение для плотности распределения времени до первого отказа принимает вид

Для однородного процесса деградации диффузионного типа коэффициент диффузии имеет простую связь с обычно используемыми характеристиками процесса – средним квадратическим отклонением скорости процесса σ и коэффициентом вариации процесса ν:

(4.17)

С учетом соотношения (4.17) выражение для закона распределения времени до отказа изделия имеет вид

(4.18)

Полученное диффузионное (diffusive) распределение (4.18), соответствующее немонотонному (nonmonotonic) марковскому процессу, по первым буквам определяющих слов называют DN-распределением.

Плотности (4.18) соответствует функция распределения

где

– нормированная функция Лапласа (интеграл вероятности).

Математическое ожидание и дисперсия времени до отказа равны соответственно

(4.19)

(4.20)

Из соотношений (4.19) и (4.20) коэффициент вариации распределения времени до отказа равен коэффициенту вариации процесса деградации:

Коэффициенты асимметрии и эксцесса DN-распределения определяются из выражений

Авторы работы [31] отмечают важное свойство, которым обладает DN-pacпределение, – устойчивость к операции свертки. Это означает, что DN-распределение может быть использовано для описания отказов при нелинейном изменении среднего значения определяющего параметра. При этом неоднородный процесс квантуется на одиночные участки и время выхода за предельный уровень получается в результате свертки времени наработки на линейных участках.