Булевы функции

Значение булевой функции F, как результат выполнения логических операций над двоичными переменными – аргументами А, В, С, ..., зависит от значения аргументов. Задать булеву функцию – значит указать значения, которые принимает функция (т.е. 0 или 1) при всех возможных комбинациях значений аргументов. Таблица, в которой построчно указываются все возможные сочетания аргументов и значения, которые булева функция принимает при каждом сочетании, называется таблицей истинности. Так, например, функции ИЛИ и И имеют только два аргумента А и В, поэтому имеется четыре возможные комбинации их значений, которые представлены в их таблице истинности (см. табл. 3.3).

Каждую конкретную комбинацию аргументов называют набором. Для краткости набор записывают в виде двоичного числа, цифрами которого являются значения аргументов. Для п аргументов существует N = 2n наборов.

Если неизвестно, какие значения принимает функция на всех наборах аргументов, то она называется недоопределенной, или не полностью (частично) определенной, а комбинации аргументов, для которых функция не определена, – запрещенными наборами.

Значения функции на запрещенных наборах можно задать по своему усмотрению (доопределить функцию). Этот прием используется при минимизации функций.

После того как таблица истинности составлена, находят алгебраическую форму этой логической функции. На следующем этапе функцию преобразуют в простейшую форму, которую потом реализуют с помощью соответствующих электрических схем. Логические функции записывают, как правило, в дизъюнктивной нормальной форме. При этом поступают следующим образом.

1. В таблице истинности выделяют строки, в которых булева функция имеет значение 1.

2. Для каждой такой строки составляют конъюнкцию всех входных переменных, причем записывают сомножитель без инверсии, если переменная принимает значение 1 (например, А), в противном случае записывают

сомножитель с инверсией (например, А ). Таким образом составляют столько конъюнкций всех аргументов, сколько имеется строк в таблице истинности, в которых функция равна 1. Каждая такая конъюнкция называется конституентой единицы.

Конституента единицы – это функция п аргументов, которая принимает значение, равное единице, только на одном наборе аргументов. На всех остальных наборах она равна нулю.

3. Наконец, записывая логическую сумму – дизъюнкцию всех найденных консгитуент единицы, получают искомую функцию.

Рассмотрим этот способ на примере таблицы истинности для функций F и F' (табл. 3.4).

Таблица 3.4

Набор	А	B	C	F'	F
0	0	0	0	0	0
1	0	0	1	0	0
2	0	1	0	1	1
3	0	1	1	0	0
4	1	0	0	1	1
5	1	0	1	0	0
6	1	1	0	1	1
7	1	1	1	-	0

Функция F' является недоопределенной. В строке 7 (правильнее сказать – на седьмом наборе) значение функции неопределенное. Доопределим эту функцию таким образом, чтобы она на этом наборе была равна 0 (функция F).

На наборах 2, 4, 6 функция равна единице. Прежде всего следует составить конъюнкции (конституенты единицы) для этих наборов.

Набор 2: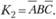

Набор 4: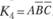

Набор 6: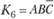

Искомая функция записывается в виде логической суммы – дизъюнкции полученных конституент единицы:

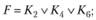
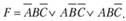
Эта запись называется совершенной дизъюнктивной нормальной формой (СовДНФ) рассматриваемой логической функции.

Минимизация булевых функций

После получения алгебраической формы записи логической функции переходят к ее упрощению или, как говорят в булевой алгебре, к минимизации.

Минимизация булевых функций производится с помощью теорем алгебры логики. Наиболее эффективными приемами минимизации являются вынесение за скобки общих членов, применение двойного отрицания, теоремы де Моргана, законов поглощения и склеивания. При этом наряду с полным склеиванием часто применяют неполное склеивание, при котором оба члена, участвовавшие в склеивании, или один из них остаются и могут склеиваться с другими конституентами. Неполное склеивание можно рассматривать как сочетание теоремы 15 с теоремой 3.

Рассмотрим процесс минимизации на примере функции F. Сначала определим, какие конституенты имеют общие члены. Это конституенты К2 и К6, а также К4 и К6.

Так как конституенты К2 и К6 имеют общие члены 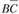, они могут быть вынесены за скобки:

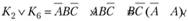
Оставшееся в скобках выражение 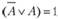. Таким образом, конституенты К2, и K6 склеиваются по А:

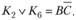
Однако конституента К6 может понадобиться для операции склеивания конституент К4 и K6, поэтому проведем неполное склеивание с сохранением конституенты K6, т.е.:

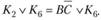
Таким образом,

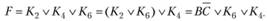
Теперь можно провести склеивание по В конституент К4 и К6:

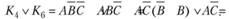
В результате имеем более простое выражение для F:

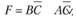
Вынесем за скобки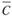и получим конечный результат минимизации: