Тарификация рисков в массовых видах рискового страхования

Тарификация рисков в массовых видах рискового страхования, для которых характерен однородный страховой портфель с большим количеством сходных по вероятности наступления и убыткам страховых рисков (автомобили, индивидуальные жилые дома и дачи, личное рисковое страхование и т.п.), включает:

1) сбор статистического материала по объектам страхования и произошедшим страховым случаям за прошлый (так называемый расчетный или тарифный) период и проверку его однородности для включения в одну тарифную группу договоров (объектов страхования);

2) определение частоты р страхового события как частного отделения числа страховых событий т (например, числа пожаров) на общее число объектов страхования п (например, число застрахованных строений) для вида страхования (тарифной группы);

3) определение математического ожидания М(u) и среднего квадратического отклонения величины страхового убытка (страховой выплаты) σ(u) в страховых случаях и средней страховой суммы на один договор страхования s для вида страхования известными из математической статистики методами в зависимости от вида статистической совокупности;

4) расчет основной части тарифа;

5) расчет рисковой надбавки;

6) расчет нетто-тарифа как суммы основной части и рисковой надбавки;

7) расчет брутто-тарифа, включающего РВД, приходящиеся на один договор.

Для статистической совокупности страховых случаев, не имеющей выраженных изменений во времени, основная часть нетто-тарифа пропорциональна частоте возникновения убытков (страховых случаев) и их средней тяжести.

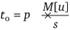. (4.5)

При возможности определения из имеющейся статистики страховых случаев величины среднего квадратичного отклонения убытка σ(u) и для однородных рисков, суммарный убыток от которых подчиняется нормальному закону, величина рисковой надбавки Тр определяется по известной формуле

, (4.6)

где α(γ) – коэффициент (квантиль распределения), зависящий от выбранного значения доверительной вероятности γ.

Пример значений коэффициента приведен в табл. 4.1.

Таблица 4.1. Значения квантиля распределения в зависимости от доверительной вероятности

Доверительная вероятность γ	0,84	0,90	0,95	0,95	0,9986
Квантиль α(γ)	1,0	1,3	1,645	2,0	3,0

В данном случае доверительная вероятность является вероятностью, с которой суммарные страховые убытки в планируемом периоде не превысят величины суммарной страховой премии, т.е. вероятностью, что страховщик не разорится.

Если величины убытка и его среднего квадратического отклонения неизвестны (при тарификации новых видов страхования), то рисковую надбавку можно приближенно рассчитать по следующей формуле:

. (4.7)

После расчета тарифа величина страховой премии определяется умножением тарифа на величину страховой суммы.

Для статистической совокупности с явно выраженным временным трендом (временного ряда) и однородными рисками с единичными убытками u вместо оценки вероятности прогнозируется число страховых случаев т на планируемый период с помощью, как правило, экспоненциальных и полиномиальных трендов второй и третьей степени. В этом случае страховой нетто-тариф определяется по формулам:

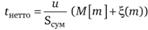; (4.8)

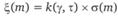, (4.9)

где k(γ,τ) – коэффициент, учитывающий относительную величину доверительного интервала изменений случайных значений числа прогнозируемых страховых случаев; σ(m) – среднее квадратическое отклонение числа прогнозируемых страховых случаев, определяемое из сравнения расчетного (прогнозного) и фактического временного ряда страховых случаев.

В работах по эконометрии показано, что при условии нормального распределения ошибок статистических наблюдений числа страховых случаев по годам (это условие выполняется в связи с большим числом ежегодных страховых случаев) доверительный интервал возможных отклонений результатов прогноза имеет распределение Стьюдента. Тогда коэффициент k(γ,τ) является квантилем распределения Стьюдента k(γ, τ – 1 – r) и определяется в зависимости от заданного значения доверительной вероятности γ, продолжительности статистических наблюдений по годам τ и числа определяемых параметров случайной функции распределения страховых случаев r (в нашем случае r = 2, поскольку мы вычисляем только математическое ожидание и дисперсию страховых случаев) по известным статистическим справочникам.

Брутто-тариф обычно определяется делением нетто-тарифа на (1 – ώ), где ώ – относительная доля РВД в структуре тарифа.