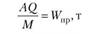Расчет некоторых параметров модели транспортного обслуживания потребителей

Для определения текущего потенциала рынка в регионе известна динамика объема спроса на продукцию за 2008– 2012 гг. (табл. 11.2). Известна также емкость рынка Ае = = 1000 усл. ед., а минимальный объем на рынке С = 100 усл. ед.

Таблица 11.2

Динамика объема спроса продукции па рынке

Годы	2008	2009	2010	2011	2012
Объем спроса в регионе, усл. ед.	120	180	580	910	960

Решение.

Объем спроса продукции на рынке переносим на график (рис. 11.6), который свидетельствует, что динамика спроса продукции соответствует логистической функции, так как имеет форму латинской буквы S, положенной набок.

Рис. 11.6. График изменения спроса продукции на рынке в регионе (логистическая функция):

– фактический текущий потенциал рынка;

– теоретический текущий потенциал рынка

Используя логистическую функцию, определим:

1. Теоретическую закономерность объема спроса.

2. Момент перехода возрастающей скорости объема спроса в убывающую, т.е. текущий потенциал рынка.

Кривая (см. график) имеет две точки перегиба и характеризуется переходом от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста к замедляющемуся (выпуклость).

Период А–В. Характеризуется незначительным ростом спроса на продукцию (180 – 120 = 60 усл. ед.).

Период В–С. Заметен ускоряющий рост спроса на продукцию (580 – 180 = 400 усл. ед.). Это связано с маркетинговым давлением, например, рекламой.

Период C–D. Намечается замедление спроса на продукцию (910 – 580 = 330 усл. ед.).

Период D–E. Резкое замедление спроса на продукцию (960 – 910 = 50 усл. ед.).

В основе логистической функции, как отмечалось выше, лежит закономерность, выраженная уравнением Ферхюльста, формула (11.2):

Используя формулу (11.5) найдем параметры а и b

Для составления системы нормальных уравнений рассчитаем по табл. 11.3 величины .

Таблица 11.3

Расчет данных для определения параметров а и b

X	Y	X1			lgZ	XlgZ
1	120	1	8,33	7,33	0,865	0,865
2	180	4	5,55	4,55	0,658	1,316
3	580	9	1,72	0,72	-0,142	-0,0426
4	910	16	1,09	0,09	-1,045	-4,180
5	960	25	1,04	0,04	-1,037	-5,185
Σ15	2750	Σ55	-	-	-Σ0.701	-Σ7.61

Из уравнений (11.5) и по данным табл. 11.3 получаем систему уравнений

Из этих уравнений получаем параметры: а = 1,5089; b = -0,5497.

Все полученные и известные параметры подставляем в формулу (11.2) (логистическая функция) и получаем теоретический объем спроса (табл. 11.4):

Таблица 11.4

Расчет теоретического значения объема спроса на продукцию

X
1	0,9592	9,1033	10,1033	99,0
2	0,4095	2,5674	3,5674	280,0
3	-0,1402	0,7241	1.7241	588,0
4	-0,6899	0,20422	1,2042	833,0
5	-1,2396	0,05759	1,05759	952,0
				Σ2752
				Факт Σ2750

Сравнивая теоретические значения (ух) с фактическим: (у), видим, что они достаточно полно согласуются между собой (см. табл. 11.2 и 11.4, т.е. 2752 и 2750).

Найдем точку перегиба – момент перехода возрастающей скорости в убывающую:

1) через сколько лет этот перегиб произойдет?

2) какой будет текущий потенциал?

Определим рациональный радиус действия регионального склада. Известны издержки склада, расстояние перевозки и объем материалопотока (табл. 11.5). Рациональный

радиус действия склада определяется на пересечения предельных и средних издержек, а также предельного дохода.

Таблица 11.5

Постоянные, переменные, общие, средние и предельные издержки

2	10	60	200	230	430	23,0	43,0	43
3	20	140	200	330	530	16,5	26,5	10
4	30	228	200	450	650	15,0	21,6	12
5	40	338	200	580	780	14,5	19,5	13
6	50	450	200	725	925	14,5	18,4	10
7	60	600	200	880	1080	14,6	18,0	15,5
8	70	700	200	1060	1260	15,1	18,0	18
9	80	768	200	1260	1460	15,7	18,2	20
10	90	819	200	1470	1670	16,3	18,5	21
11	100	780	200	1700	1960	17,0	19,0	23

Примечание.

где – общие издержки и расстояние перевозок в рассматриваемом периоде соответственно; – общие издержки и расстояние перевозок в периоде п – 1 соответственно.

Построим график предельного дохода, предельных издержек, средних общих издержек (рис. 11.7), на котором легко определить точку пересечения этих трех показателей. Итак, рациональный радиус действия предприятия равен 70 км, так как именно в этой точке .

Сравнивая валовой доход с валовыми издержками, находим, что максимальная прибыль, которую может получить склад (фирма), равняется 168 усл. ден. ед. при перевозке 700 и 600 усл. ед. продукции (табл. 11.6). Предприятие будет работать с прибылью при радиусе в 50 и 60 км. 50 км является предельным расстоянием, если рациональный радиус предприятия уменьшить, а если будет меньше, чем 50 км, то предприятие понесет убытки (см. табл. 11.5).

Рис. 11.7. Определение рационального радиуса действия фирмы в зависимости от предельных и средних издержек:

Ro – рациональный радиус действия регионального склада; Rn – предельный радиус действия регионального склада

Таким образом, мы смогли определить рациональный радиус действия склада по обслуживанию потребителей и тариф, при котором будет обеспечена нормальная прибыль. Тариф за единицу продукции будет равен 204 усл. ден. ед. (см. табл. 11.6).

Эффективная работа склада связала с определением оптимального количества автомобилей, которые ежедневно поступают на обслуживание, и закон, по которому происходит это поступление.

Оптимальное количество автомобилей, которое должно обслуживать региональный склад, определено с использованием закона убывающей отдачи (табл. 11.7), а методы теории вероятности используются для выявления закона поступления автомобилей.

Таблица 11.6

Сопоставление валового дохода с валовыми издержками и предельного дохода с предельными издержками

Расстояние, км	Объем материалопотока, усл. ден. ед.	Тариф, усл. ден. ед.	Валовой доход, усл. ден. ед.	Предельный доход	Издержки, усл. ден. ед.				Прибыль (+), условные убытки (-)
					средние перемен ные	средние общие	общие	предельные
10	60	2,60	156,0	15,6	23,0	43,0	430	43,0	-274,0
20	140	2,50	350,0	19,4	16,5	26,5	530	10,0	-180,0
30	228	2,40	547,2	19,7	15,0	21,6	650	12,0	102,8
40	336	2,30	772,8	22,5	14,5	19,5	780	13,0	-7,8
50	450	2,20	990,0	21,7	14,5	18,4	925	14,5	+70.0
60	600	2,08	1248,0	25,8	14,6	18,0	1080	15,5	+ 168,0
70	700	2,04	1428,0	18,0	15,1	18,0	1260	18,0	+ 168,0
80	768	2,00	1536,0	10,8	15,7	18,2	1460	20,0	+76,0
90	819	1,90	1556,1	2,0	16,3	18,3	1670	21,0	-113,9
100	780	1,80	1404,0	-15,2	17,0	19,0	1900	23,0	-496,0

Таблица 11.7

Расчет оптимального количества автомобилей для обслуживания регионального склада

Количество занятых автомобилей, А, шт.	Суточный объем перевозок, Q, усл. ед.		Средняя производительность автомобиля,	Предельная производительность автомобиля,
1	2		3	4
0	0		0	0
5	25	25	5	5
10	65	40	6,5	8
15	115	50	7,67	10
20	190	75	9,5	15
25	250	60	10	12
30	300	50	10	10
35	340	40	9,71	8
40	375	35	9,38	7
45	405	30	9	6
50	430	25	8,6	5
55	450	20	8,16	4

Первый столбец таблицы доказывает количество занятых автомобилей для перевозки продукции А, во втором – суточный объем перевозок Q, в третьем – средняя производительность автотранспортного средства (определяется как отношение суточного объема перевозки к числу занятых автомобилей для перевозки продукции, т.е. ), а в четвертом – предельная производительность автотранспортного средства.

Из табл. 11.7 очевидно, что при увеличении числа занятых автомобилей А суточный объем перевозок растет, средняя производительность автомобиля растет до тех пор, пока количество занятых автомобилей не достигнет 25 ед., затем некоторое время держится на уровне, близком к постоянному, а при дальнейшем увеличении А падает. Предельная производительность автомобиля ведет себя аналогично , но быстрее достигает максимального значения.

Когда средняя величина производительности автомобиля достигает максимального уровня, его предельная производительность в этот момент принимает тоже численное значение. Из табл. 11.7 видим, что, когда средняя производительность автомобиля достигает максимума = 10 т (при количестве автомобилей, равном 30 ед.), предельная производительность автомобиля равна этой же величине. Равенство этих величин считается оптимальным вариантом.

Следовательно, оптимальным вариантом для нашего случая следует считать 30 автомобилей, а суточный объем 300 т.