Практическое применение уравнения Бернулли

Уравнение Бернулли имеет широкое применение во многих гидравлических расчетах и для объяснения многих гидравлических явлений. В частности, оно может быть использовано при измерении давления и скорости движущейся жидкости. Для измерения давления используется пьезометр (прямая трубка на рис. 4.31). Для измерения скорости совместно с пьезометром используется трубка Пито – трубка полного напора. Она представляет собой трубку, изогнутую под прямым углом и установленную навстречу потоку.

Рис. 4.31. Схема определения скорости течения жидкости с помощью пьезометра и трубки Пито

Уровень жидкости в пьезометре равен

Разность уровней в пьезометре и в трубке полного напора будет равна скоростному напору

Действительно, запишем уравнение Бернулли для точек А и В:

Так как , , , то , где

– высота жидкости в трубке полного напора;

– высота жидкости в пьезометре.

Отсюда

Тогда

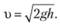
За счет вязкости жидкости и других отклонений от идеального случая преобразования энергии обычно , поэтому, чтобы не получать пониженных значений скоростей, вводится коэффициент , определяемый для каждой трубки опытным путем:

Трубка Пито – Прандтля

Дальнейшим усовершенствованием трубки Пито является трубка Пито – Прандтля. В этом приборе объединяются трубка Пито и пьезометр (рис. 4.32). Роль трубки Пито здесь выполняет трубка 2 (она направлена навстречу потоку), а пьезометра – трубка 1 (отверстия в этой трубке находятся параллельно направлению потока).

Рис. 4.32. Трубка Пиго – Прандтля

Пусть в сечении I имеем давление и скорость набегающего потока р и и. В сечении II давление на входе в трубку 2 равно(скоростьздесь равна нулю). Записывая уравнение Бернулли для сечений I и II и учитывая, что, , получаем

Отсюда

(4.25)

Для определениявоспользуемся формулой гидростатического давления(см. параграф 3.6).

Применяя эту формулу для точек А и D, получаем

где– удельный вес ртути;– удельный вес газа, скорость которого измеряется.

Так как при равновесии давление в точках А и D одинаково, то

Учитывая, что получаем

Подставляя последнее соотношение в формулу (4.25), находим

Для каждой отдельной трубки вводится некоторый коэффициент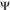, определяемый опытным путем. Поэтому формула для определения скорости потока принимает вид

Трубка Вентури, сопло, диафрагма

В промышленных условиях для измерения расхода жидкостей применяются трубки Вентури, сопла и диафрагмы. Более подробно рассмотрим трубку Вентури (рис. 4.33). Трубка Вентури создаст в трубопроводе местное сужение потока и по возникающему перепаду давлений Δр можно определить расход жидкости.

Для сечений I и II запишем уравнение Бернулли (считая распределение скоростей равномерным)

где – потеря напора между сечениями I и II, ; – коэффициент местных потерь (см. параграф 6.15). Уравнение неразрывности для несжимаемой жидкости имеет вид .

Отсюда

Подставляя,, и в уравнение Бернулли и выражая, получаем

Рис. 4.33. Трубка Вентури

Рис. 4.34. Схема распределения скоростей и давлений в трубке Вентури с дифференциальным трубным манометром

Объемный расход будет определяться по формуле

(4.26)

где С – величина, постоянная для данного расходомера (трубки Вентури).

Довольно часто вместо пьезометров для измерения перепада давления в расходомере применяют дифференциальный трубный манометр (рис. 4.34).

Учитывая, что над ртутью в трубках находится одна и та же жидкость плотностью ρ, можно записать

(4.27)

Значения Δh, полученные по формуле (4.27), можно использовать для определения расхода по формуле (4.26).

Аналогично для измерения расхода могут быть использованы диафрагмы (рис. 4.35) и сопла (рис. 4.36).

Рис. 4.35. Диафрагма

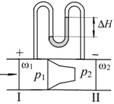
Рис. 4.35. Сопло