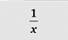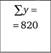Методика расчетов оптимальных размеров складских предприятий

Важным моментом при проектировании склада является не только экономическое обоснование создания складского предприятия, но и определение его оптимального размера. Критерием выбора оптимального размера склада могут быть суммарные затраты, которые складываются из себестоимости складской переработки 1 т продукции (), транспортных расходов, связанных с доставкой 1 т продукции потребителям (), и удельных капитальных вложений () на единицу годовой мощности склада. Этот критерий выражается следующим образом:

где 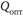– оптимальный размер склада. Он выбирается по минимальным затратам, но которые определены критерием выбора.

Для исчисления элементов критерия воспользуемся табл. 7.5.

Таблица 7.5. Исходные данные для расчета (условные)

Годовой объем складского товарооборота, т	Себестоимость 1 т складской переработки продукции, усл. ед./1 т	Транспортные издержки на 1 т перевозимой продукции, усл. ед./1 т	Капитальные вложения, млн усл. ед.	Удельные капитальные вложения на единицу годовой мощности склада, усл. ед.
10 000	250,0	10,0	6000,0	600,0
30 000	180,0	16,0	12 000,0	400,0
50 000	150,0	22,0	15 000,0	300,0
70 000	140,0	27,0	17 500,0	250,0
100 000	100,0	35,0	20 000,0	200,0

Исходные данные представляются динамическими рядами, которые являются статистическими показателями, характеризующими экономические изменения по времени. По исходной информации строится ранжированный ряд, который располагается либо в порядке возрастания, либо в порядке убывания размера склада. Далее определяется характер зависимости, которая описывается математически.

Часто зависимость затрат носит нелинейный характер и приближается к кривой типа гиперболы: 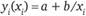. Вычисляют параметры а и b по способу наименьших квадратов, используя для этого систему нормальных уравнений.

Начнем с определения первого элемента критерия – себестоимости складской переработки 1 т продукции:

Эмпирическая линия регрессии (рис. 7.4) по своему характеру весьма близка к кривой типа гиперболы и описывается уравнением

Годовой объем складского товарооборота, тыс. т Рис. 7.4. Эмпирическая и теоретическая линии регрессии, характеризующие себестоимость переработки 1 т продукции

Используя способ наименьших квадратов, получаем систему нормальных уравнений:

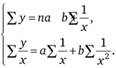
При определении сумм показателей, входящих в уравнения, используем данные табл. 7.5 и рассчитанные на их основе данные табл. 7.6.

Таблица 7.6. Данные для определения параметров а и b

x – годовой объем складского товарооборота, т	у – себестоимость 1 т складской переработки продукции, усл. ед./1 т
10 000	250,0	0,00010	0,000000010	0,025	250,1
30 000	180,0	0,000033	0,00000000108	0,006	161,2
50 000	150,0	0,000020	0,0000000004	0,003	143,4
70 000	140,0	0,000014	0,00000000019	0,002	135,8
100 000	100,0	0,000010	0,0000000001	0,001	130,1
п = 5					820,6

Подставим соответствующие значения в систему уравнений и определим параметры а и b.

В результате получаем

Таким образом, формула, определяющая гиперболу, после определения параметров а и b будет Вперед:

Далее рассчитаем себестоимость С1т (складская переработка продукции) с помощью полученной формулы. Эти данные приведены в табл. 7.5.

Используя данные параметры и формулу гиперболы, можно определять себестоимость 1 т складской переработки продукции () для любого варианта размера склада. Например, требуется определить себестоимость 1 т складской переработки продукции с годовым объемом в 120 тыс. или 150 тыс. т. Подставив в уравнение гиперболы значение параметров, получим:

Перейдем к исчислению второго элемента критерия – транспортных расходов. Графическая зависимость транспортных расходов (рис. 7.5) близка к линейной и описывается уравнением

Система нормальных уравнений имеет следующий вид:

Подставим полученные величины из табл. 7.5, получаем

Рис. 7.5. Эмпирическая и теоретическая линии регрессии, характеризующие транспортные расходы

Таблица 7.7. Расчетные данные для определения параметров а и h

x – годовой объем складского товарооборота, т	у – транспортные расходы на 1 т, усл. ед.	x2	ху
10 000	10,0	100 000 000	1 000 000	10,7
30 000	16,0	900 000 000	480 000	16,1
50 000	22,0	2500 000 000	1 100 000	21,5
70 000	27,0	4900 000 000	1 890 000	26,9
100 000	35,0	10 000 000 000	3 500 000	35,0
п = 5 Σx= 260 000	Σy= 110,0	Σx2 = 18 400 000 000	Σxy= 7070000	110,2

Поделив первое уравнение на 5, а второе на 260 000, получим следующие уравнения:

Из этих уравнений получаем параметры ат и bт:

Уравнение прямой

В последнем столбце табл. 7.7 приведены транспортные расходы (теоретическая кривая).

Определим транспортные расходы на единицу продукции для складских хозяйств с объемом товарооборота в 120 тыс. и 150 тыс. т:

Следует отметить, что указанные расчеты сделаны применительно к автомобильному транспорту.

Далее рассчитаем третий элемент критерия – удельные капитальные вложения, умноженные на коэффициент эффективности. Графическая зависимость удельных капитальных вложений от размера складского товарооборота (рис. 7.6) Вперед.

Эмпирическая линия регрессии, характеризующая зависимость от размера складского товарооборота, является гиперболой, описывается уравнением и приведена на рис. 7.6.

Рис. 7.6. Эмпирическая и теоретическая линии регрессии, характеризующие удельные капитальные вложения

Система нормальных уравнений будет иметь следующий вид:

Необходимые величины для решения этой системы рассчитаны на основе исходных данных (см. табл. 7.5) и приведены в табл. 7.8.

Используем полученные величины для решения системы уравнений:

В результате получим

Таблица 7.8. Исходные данные для расчета

X – объем складского товарооборота, т	Ук(х) – удельные капиталовложения, усл. ед.
10 000	600,0	0,000100	0,00000001000	0,0600	601,0
30 000	400,0	0,000033	0,00000000108	0,0130	340,0
50 000	300,0	0,000022	0,00000000048	0,0060	288,0
70 000	250,0	0,000014	0,00000000061	0,0035	265,0
100 000	200,0	0,000010	0,00000000010	0,0020	249,0
					1753,0

По этим параметрам уравнение гиперболы будет

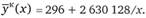
Найденные параметры дают возможность определить удельные капитальные вложения для любого возможного варианта размера складского хозяйства, например для складского предприятия с годовым объемом товарооборота 120 тыс. и 150 тыс. т. Они будут равны:

Теперь у нас есть все необходимые данные для того, чтобы по избранному критерию определить суммарные затраты по каждому варианту размера складского предприятия, в том числе и таких размеров, которые будут создаваться в перспективе (табл. 7.9).

Данные табл. 7.9 показывают, что оптимальным вариантом является складское предприятие с объемом годового товарооборота 100000 т, поскольку суммарные затраты являются минимальными из всех рассматриваемых вариантов.

Необходимо отметить, что окупаемость капитальных вложений складских предприятий разных размеров, как показывают расчеты, неодинаковая. С уменьшением размера складского предприятия технологическая структура капитальных вложений становится менее совершенной. Удельный вес оборудования снижается, а удельный вес строительно-монтажных работ и, следовательно, пассивной части основных фондов (в части зданий) растет. И наоборот, чем крупнее складское предприятие, тем прогрессивнее технологическая структура капитальных вложений. Имеет значение и то, что затраты труда на единицу складской продукции на крупных складских предприятиях намного ниже, а уровень производительности труда более высокий. Все это ведет к тому, что по мере увеличения складского производства срок окупаемости сокращается.

Таблица 7.9. Выбор оптимального варианта складского хозяйства

Варианты	Годовой объем складского товаро оборот, т	Себестоимость складской переработки 1 т продукции, усл. ед.	Транспортные расходы, связанные с доставкой 1 т продукции, усл. ед.	Показатели капитальных вложений
				удельные	Е1 – коэффициент эффективности	удельные, умноженные на Е	суммарные затраты, усл. ед.
1	10 000	250,1	10,7	601,0	0,2	120,2	381,0
2	30 000	161,2	16,1	340,0	0,2	68,0	244,3
3	50 000	143,4	21,5	288,0	0,2	57,6	222,5
4	70 000	135,8	26,9	265,0	0,2	53,0	215,7
5	100 000	130,1	35,0	249,0	0,2	49,8	214,9
6	120 000	127,9	40,4	242,6	0,2	48,4	216,7
7	150 000	125,6	48,5	236,0	0,2	47,2	221,3
8	200 000	123,4	62,0	229,5	0,2	45,9	231,3
9	250 000	122,1	75,5	225,6	0,2	45,12	242,72

1 E – коэффициент эффективности в расчетах принимаем 0,2, т.е. срок окупаемости склада должен составить пять лет.