Кривые издержек в краткосрочном периоде

Зная цены ресурсов и зависимость объемов производства от количества используемых ресурсов, можно вычислить издержки производства. Рассмотрим следующую ситуацию. Будем полагать, что у фирмы постоянные издержки производства, связанные с использованием двух единиц капитала, составляют 100 тыс. руб., а заработная плата одного рабочего в неделю – 10 тыс. руб. Составим таблицу издержек фирмы с учетом условных объемов выпуска продукции (табл. 9.2).

Таблица 9.2

Издержки производства в краткосрочном периоде

Кол-во единиц труда (L)	Объем пр-ва (Q)	Суммарные издержки, тыс. руб.			Предельные издержки, тыс. руб.	Средние издержки, тыс. руб.
		TFC	TVC	ТС		AFC	AVC	АТС
0	0	100	0	100
					0,833
1	12	100	10	110		8,333	0,833	9,166
					0,333
2	42	100	20	120		2.381	0,476	2,857
					0,256
3	81	100	30	130		1,234	0,370	1,604
					0,322
4	112	100	40	140		0,892	0,357	1,249
					0,556
5	130	100	50	150		0,769	0,384	1,153
					1,250
6	138	100	60	160		0,724	0,434	1,158
					5,000
7	140	100	70	170		0,714	0,500	1,214

В табл. 9.2 суммарные постоянные издержки (TFC) неизменны для любого объема выпуска товаров. Суммарные переменные издержки (TVС) находятся как произведение количества введенных единиц переменного ресурса (труда – L) на величину заработной платы W одного рабочего, поскольку W определяет издержки фирмы на единицу переменного ресурса: TVС = L • W. Величины предельных издержек располагаются между строк таблицы, показывая, что МС отражают отношение изменений суммарных издержек к изменениям объемов выпуска продукции. Например, при вводе третьей единицы труда суммарные издержки возрастают на 10 тыс. руб., а объем производства – на 39 единиц (81–42), поэтому МС = ΔTC/ΔQ = 100/39 = 0,256 тыс. руб. При построении кривой МС соответствующие значения предельных издержек откладываются на середине отрезка ΔQ, в нашем случае величина МС = 0,256 откладывается при Q = 61,5.

На основании данных табл. 9.2 построим графики соответствующих кривых (рис. 9.1). Как следует из рис. 9.1, а, кривые суммарных издержек (ТС) и суммарных переменных издержек (TVC) отстоят друг от друга всегда на одну и ту же величину суммарных постоянных издержек TFC. Это следует из того, что ТС = TFC + TVC. Поскольку выпуск дополнительной единицы товара связан с увеличением суммарных издержек, кривая ТС всегда имеет восходящий характер при любых значениях Q.

Издержки Издержки

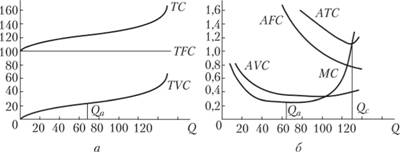
Рис. 9.1. Кривые издержек:

а – суммарных; б – предельных и средних

Иной характер у кривых средних и предельных издержек (см. рис. 9.1, б). На начальном уровне (до величины Qn, точка а кривой МС) значения предельных издержек уменьшаются, а затем начинают постоянно расти. Это происходит вследствие закона снижающейся отдачи ресурсов. Согласно этому закону, введение в производство дополнительной единицы переменного ресурса (труда) приводит сначала к росту предельного продукта. Поскольку цена единицы труда (заработная плата) постоянна, то если очередной дополнительный рабочий дает прибавку в предельном продукте, т.е. производит больше, чем его предшественник, значит, издержки производства в расчете на одну добавленную единицу товара (предельные издержки) снижаются. Когда же введение дополнительной единицы труда начнет понижать предельный продукт, предельные издержки станут расти. Отсюда следует вывод, что величины МР и МС изменяются в обратных направлениях – когда МР растет,

предельные издержки МС снижаются, а при уменьшении предельного продукта МР величины МС повышаются. Если МР достигает максимума, то МС в этот же момент имеет минимум.

Поскольку согласно закону снижения предельного продукта введение в производство дополнительных единиц переменного ресурса при наличии постоянных ресурсов непременно приводит к снижению предельного продукта МР, можно считать, что при этих условиях обязательно наступит момент, когда дальнейшее расширение производства будет сопровождаться постоянным ростом предельных издержек. В этой связи закон непременного снижения предельного продукта можно трактовать как закон непременного увеличения предельных издержек.

Аналогично можно показать, что в соответствии с законом непременного уменьшения среднего продукта сначала средние издержки будут снижаться, поскольку средний продукт растет, а затем, когда АР станет снижаться, средние издержки начнут возрастать.

До тех пор пока предельные издержки меньше средних переменных издержек, последние будут снижаться, а когда МС превысят AVС, средние издержки станут возрастать. Так как постоянные издержки не меняются, суммарные издержки АТС снижаются, пока МС меньше АТС, но они начнут повышаться, как только величина МС превысит АТС. Следовательно, линия МС пересекает кривые AVC в АТС в точках их минимума. Что касается кривой средних постоянных издержек, то, поскольку AFC = TFC/Q и TFC = const, значения AFC постоянно снижаются с ростом Q, а кривая AFC имеет вид гиперболы.

Объем выпуска, при котором достигаются наименьшие средние суммарные издержки (т.е. издержки на единицу продукции минимальны), называется производственной мощностью фирмы. Если фирма достигла производственной мощности, то из этого нс следует, что она достигает максимально возможного объема производства товаров и услуг. Фирма может и дальше расширять выпуск продукции, но это приведет к росту издержек на единицу продукции, т.е. фирма будет получать меньшую прибыль на единицу продукции (удельную прибыль). Как следует из рис. 9.1, б, в рассматриваемом примере фирма достигает производственной мощности, выпуская Q. единиц товара. Если фирма производит товар в объемах, меньших Q., то считается, что она действует с избыточной производственной мощностью.

Все семейство кривых издержек было построено на предположении, что фирма использует две единицы капитального ресурса и ее постоянные издержки равны 100 тыс. руб. Для любых иных величин капитальных ресурсов фирма будет иметь другие кривые издержек. Однако, как отмечалось в начале главы, изменения капитальных ресурсов происходят в долгосрочном периоде.