Биномиальная модель для нескольких периодов оценки
Усложним условия модели и представим, что инвестор в исходный момент предполагает возможность неоднократного изменения цены базовой акции до окончания опциона. Иными словами, за время существования опциона цена акции, по мнению инвестора, с вероятностью Р может достигать значения и • S и с вероятностью (1 – Р) величины d • S. Причем такие варианты возникают неоднократно. Предположим сначала, что биномиальный процесс длится два периода. Тогда возможные варианты изменения цен базовой акции и цен опциона на покупку этой акции можно представить следующим образом (рис. 6.9).
В таком случае возможные комбинации цен опциона на покупку будут представлены следующим образом (рис. 6.10).

Рис. 6.9. Возможные комбинации цен базовой акции (два шага)

Рис. 6.10. Возможные комбинации цены опциона колл
Как следует из рис. 6.10, возможны три комбинации изменения цены опциона по окончании второго шага расчета.
1.  – когда цена базовой акции дважды возрастает.
– когда цена базовой акции дважды возрастает.
2. 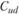 – когда цена базовой акции сначала возрастает, а затем снижается (или, что равнозначно, сначала падает, а затем возрастает).
– когда цена базовой акции сначала возрастает, а затем снижается (или, что равнозначно, сначала падает, а затем возрастает).
3.  – если цена базовой акции дважды падает.
– если цена базовой акции дважды падает.
Воспользовавшись равенством (6.6), можно представить выражение для вычисления величин  и
и  :
:

Рассмотрим теперь исходный момент и найдем цену опциона колл, зная его цены в конце первого шага расчета:

Иными словами,

Аналогичные вычисления можно провести для дерева возможных результатов любой длительности, каждый раз определяя возможные варианты цен опционов. Если известны величины и и d, а также ставки процента R, то можно найти стоимость опциона на покупку, проводя последовательные расчеты от последнего шага дерева к исходному моменту для любого количества шагов расчета.
Используя паритет опционов, можно, вычислив цену европейского опциона колл, найти цену соответствующего опциона пут.
Биномиальная модель для американских опционов
Строго говоря, биномиальная модель применима только для европейских опционов. Однако в определенных случаях ее можно распространить и на американские опционы. Так, согласно правилу 7 если американский опцион колл заключен на акции, по которым не выплачивается дивиденд, то досрочное исполнение таких опционов не оптимально. Поэтому стоимость такого американского опциона на покупку можно оценивать с использованием биномиальной модели для европейских опционов.
Но для американских опционов на покупку акций, по которым выплачиваются дивиденды, а также для американских опционов на продажу в целом (т.е. с дивидендами или без дивидендов) досрочное исполнение опционов может быть более выгодным. Возможность досрочного исполнения опционов усложняет биномиальную модель: в этом случае необходимо в каждом узле биномиального дерева возможных результатов проверять, является ли стоимость опциона выше вычисленной цены, и цена опциона будет составлять большую из этих величин.
Представим, что мы оцениваем стоимость опциона на продажу акции с текущей ценой 100 руб., по которой нс выплачивается дивиденд, для двух шагов расчета, соответствующие величины и = 1,15 и d = 0,9. Цена исполнения опциона К = 100 руб., безрисковая ставка процента Rj= 1%.
Тогда дерево возможных цен акции примет следующий вид:
Рассмотрим европейский опцион пут и оценим его стоимость: через два шага стоимость данного опциона будет Рuu= 0, если цена базовой акции вырастет до 132,25 руб., Pud= 0, если цена базовой акции станет равной 103,50 руб., и Рdd= 19 руб., если цена упадет до 81 руб. Вычислим риск-нейтральную вероятность Λ и проведем вычисление цены опциона с использованием формулы (6.6):


Рассчитаем стоимости опциона за шаг до его исполнения с использованием формулы (6.6):


Используя формулу (6.6), найдем цену европейского опциона пут в исходный момент времени:

Дерево возможных цен опциона на продажу будет иметь следующий вид:

Рассмотрим теперь американский опцион на продажу на эту же самую акцию и с теми же начальными условиями: в момент окончания опциона его цены будут теми же, что и для европейского опциона. Однако за один шаг до окончания опциона стоимость европейского и американского опциона пут может отличаться. Очевидно, что и для американского опциона на продажу его цена Рu = 0. Однако при определении цены Рd необходимо учитывать, что в этот момент цена акции d • S = 90 руб. Поэтому при немедленном исполнении американского опциона его стоимость Рd= 10 руб., а не 5,68 руб.
В связи с этим в дереве возможных результатов величина 5,68 руб. должна быть заменена на 10 руб.
Применив формулу (6.6), получим исходную стоимость американского опциона на продажу:


Значит, стоимость американского опциона на продажу оказывается выше стоимости соответствующего европейского опциона пут.