Бессрочная рента и аннуитет
Среди финансовых инструментов можно встретить такие, которые в течение неограниченного периода дают постоянный доход. Примером могут служить британские консоли (консолидированные облигации), выпущенные британским правительством еще во время войн с Наполеоном. У этих облигаций нет конечного срока обращения, и они до сих пор обращаются на британском фондовом рынке. По этим облигациям ежегодно их владельцы получают 4,5 фунта стерлингов в виде дохода. Данные ценные бумаги не имеют срока погашения и, следовательно, инвестор в течение бесконечного отрезка времени получает фиксированный годовой доход.
Фиксированные равновеликие платежи, совершаемые через одинаковые промежутки времени, в течение неограниченного срока называются бессрочной рентой.
Как определить текущую стоимость бессрочной ренты? Вернемся к нашему примеру с британскими консолями. Если известно ежегодное поступление по данной облигации, то текущая цена этой ценной бумаги определяется по формуле
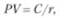
где РУ — текущая (приведенная) стоимость; С — постоянный годовой доход; г — требуемая годовая доходность (ставка дисконтирования).
Если годовая доходность, которую требует инвестор по государственным ценным бумагам британского правительства, составляет 6,5%, а по облигациям ежегодно выплачивается 4,5 фунта стерлингов (ф. ст.), то текущая стоимость облигации составит:

Формула определения текущей стоимости, как мы видим, достаточно проста. Однако насколько она корректна? Давайте проверим и выведем эту формулу из классической формулы приведенной стоимости.
1. Определим текущую стоимость будущих платежей:

2. Умножим обе части уравнения на -— :

3. В результате получим

4. Вычтем из уравнения (4.1) уравнение (4.2):

Если операция совершается на бессрочном периоде действия, т.е. п стремится к бесконечности, то выражение ———г становится бесконечно малой ветчиной, которой можно пренебречь. В этом случае мы получаем

5. Умножим обе части на (1 + г):

6. Отсюда приведенная стоимость

Аннуитет
Суть аннуитета заключается в том, что из первоначальной суммы, размещенной под определенный процент, в течение нескольких лет делаются равновеликие выплаты. К концу срока инвестор все средства выбирает и остаток средств на счете равен нулю.
Аннуитет представляет собой несколько равновеликих выплат в течение определенного числа лет.
Рассмотрим пример. Человек за изобретение получил вознаграждение в размере 10 000 долл. Он не хочет эти денежные средства тратить сразу, а намеревается использовать их в течение 10 лет равными долями. При этом, как разумный инвестор, он хочет, чтобы на неиспользуемую часть денежных средств начислялись определенные проценты. Поэтому он размещает 10 000 долл. на банковском депозите с начислением 5% годовых и предусматривает в условиях договора равномерное получение денежных средств, с тем, чтобы через 10 лет выбрать всю сумму с учетом накопленных процентов. Какую же сумму будет получать инвестор ежегодно? Ее можно вычислить на основе формулы текущей стоимости аннуитета, которая имеет следующий вид:

где РУ — текущая стоимость аннуитета; С — сумма ежегодного денежного потока; г — ставка дисконтирования; п — число лет аннуитета.
В нашем примере известно, что текущая стоимость аннуитета составляет 10 000 долл. США, которые помещаются в банк под 5% годовых на 10 лет. Следовательно, мы можем найти С, сумму годовых платежей:

Отсюда сумма ежегодных равномерных платежей составит 1295,05 долл. США.
Достаточно часто решается обратная задача, когда человек желает в течение определенного числа лет получать фиксированные равновеликие суммы. Ему требуется знать, какую сумму он должен разместить сегодня, чтобы получить желаемые средства. Примером такой ситуации может служить покупка человеком пенсионного аннуитета у страховой компании. Например, человек хочет в течение 10 лет получать ежегодно 3000 долл. он обращается в страховую компанию, которая предлагает купить страховой полис на 10 лет с начислением 15% годовых. Какую сумму необходимо внести в оплату страхового полиса? Эта сумма рассчитывается по вышеприведенной формуле

Для того чтобы не производить громадные расчеты, существуют специальные таблицы аннуитетов, которые показывают приведенную стоимость денежной единицы для каждого года. Таблица аннуитетов дана в приложении 3. Ниже приведен фрагмент таблицы аннуитетов (табл. 4.7).
Таблица 4.7. Текущая стоимость аннуитета 1 ден. ед. за период
|
Год |
Годовая процентная ставка |
||||||||||||||
|
1 |
2 |
… |
5 |
6 |
7 |
8 |
… |
15 |
|||||||
|
1 |
0.990 |
0,980 |
0,952 |
0.913 |
0,935 |
0,926 |
0,470 |
||||||||
|
2 |
1,970 |
1,942 |
1,859 |
1,833 |
1,808 |
1,783 |
1,626 |
||||||||
|
3 |
2,941 |
2,844 |
2,723 |
2,673 |
2,624 |
2,577 |
2,283 |
||||||||
|
4 |
3,902 |
3,808 |
3,546 |
3,465 |
3,387 |
3,312 |
2,855 |
||||||||
|
5 |
4,853 |
4,713 |
4,329 |
4,121 |
4,100 |
3,993 |
3,352 |
||||||||
|
10 |
9,471 |
8,983 |
7,772 |
7,360 |
7,024 |
6,710 |
5,019 |
||||||||
|
15 |
1.3.87 |
12,85 |
10.38 |
0.712 |
0.108 |
8.550 |
5.817 |
||||||||
|
20 |
18,05 |
1 (¡.35 |
12,46 |
11,47 |
10.50 |
0,818 |
6.259 |
||||||||
В нашем примере срок аннуитета составляет 10 лет, по которому выплачивается 15% годовых. Пользуясь табл. 4.7, на пересечении строки (10 лет) и столбца (15%) находим приведенную стоимость одной денежной единицы, равную 5,019. Если ежегодный платеж составляет 3000 долл., то приведенная стоимость аннуитета 3000 • 5019 = 15 057 долл.