Задача производителя
В той модели продукты питания производятся по технологии с постоянной отдачей и на совершенно конкурентном рынке. Однако производство промышленных товаров подразумевает экономию от масштаба. Самый простой способ задать такую технологию – ввести фиксированные издержки. Пусть единственный фактор производства – труд. И производство единицы каждой разновидности требует одинаковых для всех разновидностей фиксированных затрат труда F и постоянных предельныхзатрат труда 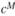 . Так что общие затраты на производство
. Так что общие затраты на производство  единиц продукции составят
единиц продукции составят

Так как потребители получают полезность от разнообразия и количество разновидностей не ограничено, то каждая существующая фирма на рынке будет производить свой продукт.
Это максимизирует готовность покупателей платить за промышленные товары.
Теперь запишем задачу максимизации прибыли фирмы, работающей в городе r (так как технология производства всех разновидностей одинакова, отличаются фирмы только местоположением):
 (6.16)
(6.16)
где  – стоимость единицы труда работников, занятых в производстве промышленных товаров в городе r, и
– стоимость единицы труда работников, занятых в производстве промышленных товаров в городе r, и  ' соответствует (6.15). Каждая фирма выбирает свою цену ФОБ
' соответствует (6.15). Каждая фирма выбирает свою цену ФОБ  , принимая индекс цен заданным. С учетом определения эластичности спроса по цене, условие первого порядка дает:
, принимая индекс цен заданным. С учетом определения эластичности спроса по цене, условие первого порядка дает:
 (6.17)
(6.17)
Пусть также вход на рынок и выход с него свободны, так что наличие положительной прибыли у фирм в каком-то городе привлекает новичков, которые снижают прибыль всем фирмам до тех пор, пока прибыль не станет равной нулю. Подставляя (6.17) в (6.16), получим это условие:
 (6.18)
(6.18)
где  – выпуск фирмы в ситуации равновесия. Заметим, что он не зависит от расположения фирмы, т.е. не зависит от размеров рынка, а только от параметров технологии и эластичности спроса. Менее эластичный спрос (при меньшей величине σ) уменьшает размеры фирм и тем самым увеличивает количество разновидностей при заданном бюджете потребителей. Чтобы это продемонстрировать явно, достаточно записать условия равновесия на рынке труда.
– выпуск фирмы в ситуации равновесия. Заметим, что он не зависит от расположения фирмы, т.е. не зависит от размеров рынка, а только от параметров технологии и эластичности спроса. Менее эластичный спрос (при меньшей величине σ) уменьшает размеры фирм и тем самым увеличивает количество разновидностей при заданном бюджете потребителей. Чтобы это продемонстрировать явно, достаточно записать условия равновесия на рынке труда.
Спрос фирмы на труд в ситуации равновесия равен
 (6.19)
(6.19)
Если в городе r предлагается  единиц труда, то число фирм в равновесии будет равно
единиц труда, то число фирм в равновесии будет равно
 (6.20)
(6.20)
Тем не менее обычно на более крупных рынках можно наблюдать более крупные фирмы, т.е. вход фирмы все-таки зависит от размера рынка. Этот эффект появляется в модели, если, например, позволить фирмам стратегическое поведение. Тогда прирост рынка распределяется между ростом фирм и их количеством. Однако для целей моделирования эффектов агломерации нам будет достаточно и упрощенной модели, представленной выше.
Уравнение для оплаты труда
Уровень оплаты труда играет важную роль в динамике моделей агломерации. Его можно выразить из условия максимизации прибыли (6.17):
 (6.21)
(6.21)
Цепа в ситуации равновесия будет такой, чтобы спрос на продукцию фирмы был равен предложению, т.е. цена должна удовлетворять уравнению (6.15) при  Выражая цену из (6.15) и подставляя в (6.21), получим уравнение для оплаты труда:
Выражая цену из (6.15) и подставляя в (6.21), получим уравнение для оплаты труда:
 (6.22)
(6.22)
Это уравнение показывает оплату труда работников, занятых в производстве промышленных товаров, при условии равновесия на рынке промышленных товаров, т.е. фирмы максимизируют прибыль, она равна нулю, а потребители максимизируют полезность с учетом бюджетного ограничения. Как видно из уравнения, оплата труда тем выше, чем ниже транспортные издержки, богаче рынки сбыта фирмы и выше уровень цен на этих рынках (ниже уровень конкуренции).
Мы также можем получить уравнение для реальной оплаты труда. Для этого номинальную оплату надо умножить на индекс стоимости жизни из (6.13) – 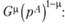
 (6.23)
(6.23)
Именно реальная оплата груда должна интересовать работников при принятии решения о переселении между городами или регионами.