Примеры применения метода дисконтирования денежных потоков

Рассмотрим примеры задач, для решения которых целесообразно использовать метод дисконтирования денежных потоков.

Пример 1. Инвестору необходимо определить рыночную стоимость облигации, по которой в начальный момент времени и за каждый квартальный купонный период выплачивается процентный доход С в размере 10% номинальной стоимости облигации N, а через два года по окончании срока обращения облигации – процентный доход и номинальная стоимость облигации, равная 1000 руб.

В качестве альтернативной схемы инвестиционных вложений предлагается банковский депозит на два года с начислением процентного дохода но схеме сложных процентных ежеквартальных выплат по ставке 8% годовых.

Решение. Для решения данной задачи используется формула (15),

где п = 8 (за два года будет осуществлено восемь квартальных купонных выплат);

β = 2% (годовая процентная ставка, равная 8%, пересчитанная на квартал);

N = 1000 руб. (поминальная стоимость облигации); C0 = С1 = С2 = ... = С7 = С= 0,1 N = 100 руб., C8 = с + N= 1100 руб.

Из формулы (15), используя условия данной задачи, для вычисления текущей стоимости облигации получаем формулу

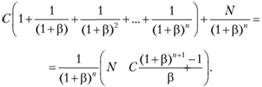
Подставляя в данную формулу числовые значения параметров, получаем текущее значение рыночной стоимости облигации, равное PC = 1686 руб.

Пример 2. Определите цену размещения коммерческим банком своих дисконтных векселей при условии, что вексель выписывается на сумму 1200000 руб. со сроком платежа 90 дней, банковская ставка – 12% годовых. Банк начисляет процентный доход ежемесячно по схеме сложного процента. Год считать равным 360 календарным дням.

Сначала решим поставленную задачу, используя общий подход (метод альтернативной доходности), который был рассмотрен ранее. Затем решим задачу методом дисконтирования денежных потоков.

Решение задачи общим методом (методом альтернативной доходности). При решении поставленной задачи необходимо учесть основной принцип, который выполняется при нормально функционирующем фондовом рынке. Он состоит в том, что на таком рынке доходность различных финансовых инструментов должна быть приблизительно одинаковой.

Инвестор в начальный момент времени имеет некоторую сумму денег X, на которую он может:

• либо купить вексель и через 90 дней получить 1200000 руб.;

• либо положить деньги в банк и через 90 дней получить такую же сумму.

Доходность в обоих случаях должна быть одинаковой.

В первом случае (покупка векселя) доход равен D = (1 200000 – X), затраты Z = X. Поэтому доходность за 90 дней равна

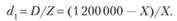
Во втором случае (размещение денежных средств на банковский депозит)

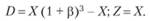
Тогда

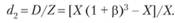
Отметим, что в данной формуле используется β – банковская ставка, пересчитанная на 30 дней, которая равна

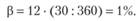
Приравнивая друг другу доходности двух финансовых инструментов (d1 = d2), получаем уравнение для вычисления X:

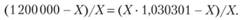
Решая это уравнение относительно X, получим X = = 1164,71 руб.

Решение задачи методом дисконтирования денежных потоков. Для решения данной задачи используем формулу (15). В ней сделаем следующие подстановки:

• процентный доход в банке начислялся в течение трех месяцев, т.е. п = 3;

• банковская ставка, пересчитанная на 30 дней, равна

• на дисконтный вексель промежуточные выплаты не производятся, т.е. С0 = С1 = С2 = 0;

• по истечении трех месяцев происходит гашение векселя и по нему выплачивается вексельная сумма, равная 1200 000 руб., т.е. С3 = 1200 000 руб.

Требуется определить, чему равна цена размещения векселя, т.е. величина РC.

Подставляя приведенные числовые значения в формулу (15), получаем уравнение PC = 1 200 000/(1,01)3, решив которое, получим

РС= 1200000 :1,030301 = 1 164,71 руб.

Как видно, для задач данного класса методы решения эквивалентны.

Пример 3. Эмитент выпускает облигационный заем на сумму 500 млн руб. сроком на один год. Купон (12% годовых) выплачивается при погашении. Одновременно эмитент начинает формировать фонд для погашения данного выпуска и причитающихся процентов, откладывая в начале каждого квартала некоторую постоянную сумму денег на специальный счет в банке, по которому банк производит ежеквартальное начисление процентов по сложной ставке 4% за год с ежеквартальными выплатами. Определите (без учета налогообложения) размер одного ежеквартального взноса, считая, что момент последнего взноса соответствует моменту погашения займа и выплаты процентов.

Решение. Эту задачу удобнее решать методом приращения денежного потока. Через год эмитент обязан возвратить инвесторам

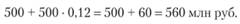
Эту сумму он должен накопить в банке до конца года. При этом инвестор осуществляет следующие вложения в банк:

1) в начале года X руб. на год под 4% годовых и ежеквартальными выплатами в банке по ставке сложного процента. С этой суммы у него в конце года будет X((1,01)4 руб.;

2) по истечении I квартала X руб. на три квартала на тех же условиях. В результате в конце года с этой суммы у него будет Х( 1,01)3 руб.;

3) аналогично вложение на полгода даст в конце года сумму X((1,01)2 руб.;

4) предпоследнее вложение на квартал даст к концу года X((1,01) руб.;

5) и последний взнос в банке в размере X совпадает по условию задачи с погашением займа.

Таким образом, осуществив денежные вложения в банк по указанной схеме, инвестор в конце года получит следующую сумму:

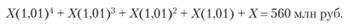
Решая данное уравнение относительно X, получаем Х= 136,552 млн руб.