Управление производственными запасами

Управление запасами в процессе функционирования компании имеет огромное значение как в технологическом, так и в финансовом аспектах.

Для финансового менеджера запасы – это иммобилизованные средства, т.е. средства, отвлеченные из оборота, объем которых логично минимизировать.

Вместе с тем объем запасов должен быть достаточным для устранения риска остановки производства в случае недопоставки сырья и материалов в соответствии с графиком технологического процесса. В этих условиях финансовый менеджмент компании должен определить оптимальный размер партии заказа (поставки) Qopt – чрезвычайно важный показатель при закупках сырья, хранении готовой продукции и транзитных запасов, например, незавершенного производства.

В основе ее решения лежит понимание разнонаправленности изменения различных затрат по мере увеличения объема закупки. С одной стороны, чем больше величина заказа, тем меньше расходы, приходящиеся на единицу ресурса при размещении заказа, в частности транспортировку. С другой стороны, увеличение объема приобретенной партии товаров вызовет рост складских расходов и потерь связанных с хранением товара.

Для вывода формулы расчета Qopt введем следующие обозначения: S – общая потребность в сырье за планируемый период времени, усл. ед.; С – затраты, связанные с хранением одной единицы сырья, ден. ед.; О – стоимость выполнения одной партии поставки, ден. ед.; Q – объем одной партии поставки, усл. ед.

Графическая иллюстрация поставки и расходования сырья в компании в условиях отсутствия резервного запаса и равномерного использования сырья можно представить на рис. 7.4.

Рис. 7.4. График поставки и расходования сырья

В предлагаемых условиях средний объем запасов в компании равен Q/2. Тогда затраты компании по содержанию запасов – С ∙ Q/2, общая стоимость выполнения заказа – О • S/Q, где S/Q число партий поставок сырья. Общие затраты компании на восполнение и хранение запасов должны быть минимизированы:

Условием экстремума рассматриваемого функционала служит равенство нулю его первой производной по параметру Q, откуда следует, что .

Рассмотренная модель в зарубежной литературе по финансовому менеджменту носит название модели наиболее экономичного размера заказа (Economic order guantity, EOG) и предполагает, что потребность остается постоянной, запасы поэтому расходуются равномерно и пополняются по мере их исчерпания.

Если эти предпосылки, упрощающие расчет оптимальной партии поставки, снять, необходимо использование более эффективных моделей, одна из которых – модель динамического программирования. В целях упрощения дальнейшего формализованного представления модели постановку рассматриваемой задачи осуществим на конкретном числовом примере^[1].

Предположим, что потребности некоторой малой фирмы в определенной продукции составляют в течение пяти периодов следующие объемы:

Перевозка этой продукции может быть осуществлена с помощью транспортного средства грузоподъемностью 100 ед. Стоимость перевозки в каждом рейсе (), где– количество перевозимой продукции (). Предполагается, что потребность производства в каждом периоде должна быть полностью удовлетворена. Если часть продукции остается на следующий период, то для хранения продукции используется склад вместимостью 50 ед. Стоимость храпения одной единицы продукции в течение одного периода – 0,2. Первоначальный запас продукции на складе предположим равен нулю (). Какое количество продукции следует перевозить в каждый период, чтобы минимизировать суммарные затраты на транспортировку и хранение этой продукции?

Решение.

Обозначим черезколичество перевозимого продукта в периоде. Остаток продукции по истечении z-го периода обозначим

Затраты за период i складываются из затрат на хранение единиц продукции, оставшейся от предыдущего периода, и затрат на перевозкуединиц продукции в течение i-го периода, т.е.

(7.1)

Для решения данной задачи воспользуемся аппаратом динамического программирования, начав решение с последнего, пятого периода.

Пятый период

Используя формулу (7.1), затраты за пятый период могут быть рассчитаны следующим образом:

К началу пятого периода остаток от предыдущего периода может быть в общем случае любым:. (Это с учетом

потребностей пятого периода:). Для уменьшения размер

ности модели расчет будем вести по дискретным точкам: 0, 10, 20, 30 и т.д. Оптимальные (в данной модели минимальные) затраты будем обозначать

Тогда для последнего (пятого) периода получим

Четвертый период

Потребность четвертого периода составляет ед. В соответствии с принципом динамического программирования оптимальные суммарные затраты за четвертый и пятый периоды могут быть рассчитаны следующим образом:

вычислены на предыдущем шаге, аможет быть рассчитана по формуле

Для

Так как потребностьединиц должна быть удовлетворена, то длявозможны следующие значения:

В этом случае

Для

Для

Третий период

где

Для

Второй период

а2 = 40.

Первый период

Очевидно, что в расчетах первого периода достаточно рассмотреть только случай, когда остаток от предыдущего периода (первоначальный запас к началу планирования) равен нулю (V0 = 0).

При этом х1 может принимать значения: 30, 40, 50, 60, 70, 80. Тогда

Итак, суммарные минимальные затраты, связанные с перевозкой и хранением запасов продукции, составят за пять периодов 63 ед. Оптимальный план, соответствующий данному результату, находится по следующему алгоритму.

1. Из последнего расчета находим

2. Анализируя , находим

3. Анализируя ', находим

4. Анализируя , находим

5. Анализируя , находим

Для удобства расчетов все промежуточные результаты удобно представить в матричном виде (табл. 7.2).

Таблица 7.2

Матрица затрат

5-й период		4-й период		3-й период		2-й период		1-й период
14	40	27	90	40	30	50	70	63	30
15	30	28	80	41	20	51	60
16	20	29	70	42	10	52	50		-
17	10	30	60	33	0	53	40	-	-
8	0	31	50	36	0	48	0	-	-
10	0	24	0	39	0	51	0

Примечание. Жирным шрифтом выделены оптимальные поставки продукции.

Ниже представлен график процесса оптимального управления запасами для рассмотренной модели (рис. 7.5).

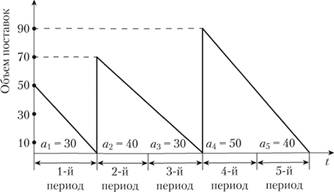
Рис. 7.5. График оптимизации производственных запасов в компании

Система JIT (Just-In-Time)

^[2]

Эффективным направлением повышения результативности управления запасами считается использование системы JIT (или "канбан" – в японском варианте), зародившаяся в компании Toyota и получившая широкое распространение во многих промышленно развитых странах. Наличие запасов в этой системе позиционируется как негативный фактор, снижающий эффективность бизнеса.

Снабжение производства организуется таким образом, когда сырье и материалы поступают в производственный процесс тогда, когда в них появляется реальная необходимость, т.е. точно в срок – в полном соответствии с названием системы. Внедрение системы JIT позволяет минимизировать незавершенное производство, товарно-материальные запасы, обеспечить выполнение заказов в четко определенное время, однако требует высочайшей производственной дисциплины и соответствующего качества организации бизнес-операций.