Учет неопределенности при планировании страхового запаса

Известно, что буфером, позволяющим в некоторой степени сгладить вариативность потребительского спроса и времени выполнения заказа поставщиком, является страховой запас, уровень которого тем выше, чем больше степень неопределенности (рис. 5.11).

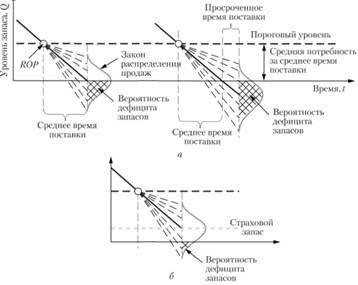
Рис. 5.11. Вероятность дефицита запасов при увеличении спроса и задержке поставки (а) и при наличии страхового запаса (б)

На рисунке сплошными линиями обозначена динамика остатков запаса исходя из предположения, что продажи будут равны среднему значению, а пунктирными – если спрос будет отличаться от него в большую или меньшую сторону.

Если значения продаж и времени выполнения заказа поставщиком распределены по нормальному закону (распределение Гаусса), то вероятности их появления будут равномерно убывать относительно среднего значения. При этом, используя среднеквадратическое отклонение (СКО, или σ), которое является мерой изменчивости (вариативности) статистического ряда, можно формировать страховой запас, соответствующий определенному уровню обслуживания (рис. 5.12):

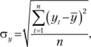(5.19)

где yt – значение параметра системы управления запасами в некоторый момент времени t; 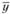– среднее значение соответствующего параметра системы управления запасами; п – количество членов в статистическом ряду параметров.

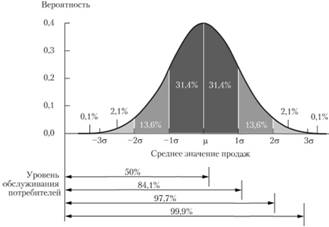
Рис. 5.12. Нормальный закон распределения продаж запасов и соответствующий уровень обслуживания

Таким образом, среднее значение параметра плюс или минус одно среднеквадратическое отклонение (±1σ) будет содержать 68% всех возможных событий (исключая по 16% с каждой стороны). Следовательно, уровни товарных запасов, сформированных таким образом, обеспечивают уровень обслуживания потребителей в 84% (в 16 случаях из 100 объем спроса или время выполнения заказа могут превысить допустимые значения, и тогда будет возможен дефицит).

Пример

В табл. 5.10 приведена статистика продаж товара за 64 дня.

Таблица 5.10

Объем продаж товара и соответствующие значения вероятности

Продажи у,, ед/день	Повторяемость, раз (дней)	Вероятность	Вероятность нарастающим итогом
60	2	0,031	0,031
70	3	0,047	0,078
80	5	0,078	0,156
90	9	0,141	0,297
100	12	0,188	0,484
110	13	0,203	0,688
120	10	0,156	0,844
130	6	0,094	0,938
140	3	0,047	0,984
150	1	0,016	1.000
Среднее значение: 105,0 ед/день	Всего: 64 дня	Итого: 1,000
СКО: 20,0 ед/день

Значения, приведенные в столбце "Вероятность", представляют собой дифференциальную функцию распределения плотности вероятностей продаж, рассчитанных, например, для 60 ед/день как 2: 64 = 0,031 и означающих, что такой объем продаж появляется с вероятностью 3,1%. Значения в графе "Вероятность нарастающим итогом" представляют собой интегральную функцию распределения и могут быть интерпретированы как вероятность того, что продажи не превысят некоторого значения. Например, вероятность того, что спрос не превысит значение 120 ед/день, составляет 84,4% (рис. 5.13).

Кроме того, полученные результаты свидетельствуют, что в 68% случаев дневные продажи не выйдут за пределы интервала 85–125 ед/день (средние продажи ±1σ). Однако для формирования запаса нас интересует только его верхняя граница.

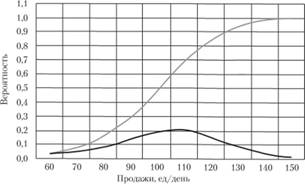
Рис. 5.13. Дифференциальная и интегральная функции распределения вероятности продаж

Допустим, что время цикла выполнения заказа поставщиком неизменно и составляет 10 дней. Тогда, исходя из среднего значения дневных продаж, объем запаса, который необходимо сформировать на это время: 105 ед/день • 10 дней = 1050 ед. При этом вероятность того, что спрос не превысит данное значение, составит 50%. Для увеличения степени удовлетворенности клиентов необходимо сформировать страховой запас исходя из следующих значений (табл. 5.11).

Таблица 5.11

Пороговый уровень запаса при различном уровне обслуживания

Уровень обслуживания, %	Уровень страхового запаса, ед/день	Число необходимых СКО (σ)	Пороговый уровень запаса, ед.
50,0	-	-	1050
84,1	20	1	1050 + 63= 1113
97,7	40	2	1050+ 126= 1176
99,9	60	3	1050+ 189=1239

Размер страхового запаса получен с учетом следующего свойства среднеквадратического отклонения:

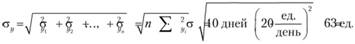
Данные вышеприведенной таблицы свидетельствуют, что лучшим решением с точки зрения минимизации затрат, связанных с запасами, является ориентация на средние продажи. Напротив, с точки зрения максимально полного удовлетворения потребительского спроса лучшим решением является формирование запаса но принципу "Средние продажи + 3σ".

Задача специалиста в области управления запасами в данном случае – определить оптимальное количество среднеквадратических отклонений для расчета страхового запаса, чтобы, с одной стороны, застраховать потери от дефицита, а с другой – не допустить резкого роста затрат на закупку и поддержание запаса на складе. Необходимость поиска баланса между этими неизбежными потерями заключается в нахождении оптимального уровня обслуживания клиентов.

Расчет уровня обслуживания можно производить разными способами. Рассмотрим вероятностный подход, который заключается в соотнесении потерь от дефицита запаса и стоимости его поддержания на складе. Представим потери от дефицита (H) следующим выражением:

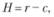(5.20)

где r – цена продажи единицы запаса покупателям компании; с – цена закупки единица запаса у поставщика (производителя).

Тогда оптимальный уровень обслуживания будет определяться отношением Н / (Н + I), где I – стоимость поддержания единицы запаса на складе компании, которое в теории управления запасами еще называют критическим (critical ratio), а соответствующий уровень запаса следующим выражением:

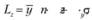(5.21)

где Lz – объем запаса при соответствующем уровне обслуживания за время выполнения заказа; σy – число единиц страхового запаса за время выполнения заказа;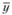– среднее значение продаж; п – число дней (время) выполнения заказа; z – количество σy, соответствующее заданному уровню обслуживания (площадь под кривой нормального распределения продаж), определяемое по табл. 5.12.

Таблица 5.12

Значения нормального закона распределения (фрагмент)

2	0,00	0,01	0,02	0,03	0,04	0,05
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199
0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596
0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987
0,3	0,6179	0,6217	0,6255	0,6293	0,6131	0,6368
0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736
0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088
0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422
0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734
0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023
0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531

Пример

Дополним условия предыдущего примера следующими данными:

– цена продажи единицы запаса покупателям (r) – 50 руб/ед.;

– цена закупки единицы запаса у поставщика (с) – 30 руб/ед.;

– стоимость поддержания единицы запаса на складе (I) – 5 руб/ед.

Тогда по критическому отношению, оптимальный уровень обслуживания составит:

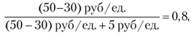
или 80%. Графическая интерпретация представлена на рис. 5.14.

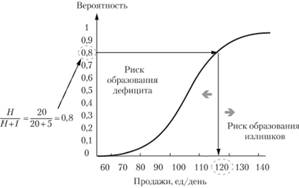
Рис. 5.14. Определение объема страхового запаса но оптимальному уровню обслуживания с использованием интегральной функции распределения вероятности продаж

Для некоторых товарных категорий потери, связанные с излишками запасов по окончании периода продаж, возникают вследствие необходимости их реализации по цене, которая может быть ниже рыночной (или себестоимости), а также в результате необходимости списания (утилизации). Примерами таких товаров могут быть продукты питания или лекарственные препараты с ограниченным сроком годности.

В этом случае для определения уровня обслуживания может быть использована модель, которая называется однопериодной. В этом случае критическое отношение должно быть дополнено потерями от уценки (списания запасов) (А):

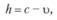(5.21)

где υ – цена продажи единицы уцененного запаса (излишков) покупателям (h = 0 – по себестоимости, h = с – если утилизировали).

Пример

Рассчитаем объем страхового запаса для условий предыдущего примера с учетом оптимального уровня обслуживания 80%.

По табл. 5.12 определяем параметр (г), для чего находим значение, максимально близкое к обслуживанию 80% (или 0,8) – это 0,7995, которое находится на пересечении строки "0,8" и столбца "0,04". Таким образом, z = 0,84. Иными словами, размер страхового запаса, который необходимо сформировать на время выполнения заказа поставщиком, составит 0,84σ, или 0,84 • 63 ед. = 52,9 ед. Тогда общий уровень запаса можно вычислить по формуле (5.21):

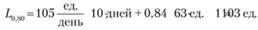
Если изменчив не только спрос, но и время выполнения заказа поставщиком, для расчета страхового запаса может быть использована Вперед зависимость:

(5.22)

где 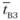– среднее время выполнения заказа (запаздывания поставки); 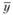– средний объем продаж; 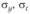– среднеквадратические отклонения продаж и времени выполнения заказа соответственно.

Пример

Дополним условия предыдущих примеров статистикой времени выполнения заказов поставщиком за 16 циклов (табл. 5.13).

Таблица 5.13

Время выполнения заказа поставщиком

Время выполнения заказа tвз, дней	Повторяемость, раз
7	1
8	2
9	3
10	4
11	3
12	2
13	1
Среднее значение – 10 дней	Всего – 16 раз
СКО (σt) – 1,6 дня

По формуле (5.22) находим значение стандартного отклонения, с помощью которого определяем размер страхового и максимального запасов для различных уровней обслуживания, в том числе для 80% (табл. 5.14):

дней 202 ед/день 1052 ед*/день • 1,62 дня * 108 ед.

Таблица 5.14

Значения порогового и страхового запаса при различных уровнях обслуживания потребителей

Уровень обслуживания, %	Страховой запас, ед.	Число необходимых σ	Пороговый уровень запаса, ед.
50,0	-	-	1050
80,0	151	0,84	1050+ 151 = 1201
84,1	180	1	1050+ 180= 1230
97,7	360	2	1050 + 360= 1410
99,9	540	3	1050 + 540= 1590

Стоит отметить, что снизить неопределенность времени выполнения заказа можно, в том числе оценивая поставщиков по надежности поставок или по точности выполнения принятых ими на себя договорных обязательств (мониторинг отношений). Очевидно, что оценка по такому критерию разделит поставщиков на несколько категорий, например надежных, условно надежных и ненадежных. Сокращая объемы закупок у последней категории поставщиков, можно добиться частичного снижения изменчивости времени выполнения заказа и сокращения объемов страховых запасов.