Территориальная конкурентоспособность и эндогенное развитие

В основе неоклассического подхода лежит понятие совокупной производственной функции. В экономике, в которой не наблюдается технический прогресс, выпуск продукции зависит от использования капитала и рабочей силы. Отношение между ними может быть описано формулой

(5.6)

где Y – выпуск; К – капитал; L – рабочая сила; F – совокупная производственная функция.

Специфической и наиболее распространенной формой этого тождества является функция производства Кобба – Дугласа:

(5.7)

где А и – параметры, которые необходимо рассчитать на основе статистических данных (обычно при помощи регрессионного анализа).

Из этого соотношения вытекает формула для производительности труда (у):

(5.8)

где k – капиталовооруженность труда.

Формула производства надушу населения показывает, что производительность может расти, только если доля капитала, приходящаяся на одного работника (т.е. капиталовооруженность труда) повышается.

Таким образом, капитал должен расти быстрее, чем рабочая сила, заставляя тем самым расти производительность работника.

Данное отношение отражено на рис. 5.3.

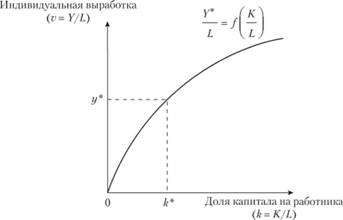
Рис. 5.3. Зависимость между производительностью и капиталовооруженностью труда

Y = F(K,L) подразумевает Y/L = f(K / L) при условии что F(K,L) однородна в первой степени.

Производственная функция Кобба – Дугласа с постоянной отдачей в масштабе часто используется в моделях роста.

Производительность повышается, если каждый из работников получает бо́льший доступ "основным фондам" – процесс, известный как интенсивное увеличение капитала.

Когда добавочный продукт рабочей силы падает до критического уровня, чистые инвестиции стремятся к нулю, и валовые инвестиции обеспечивают лишь поддержание существующего запаса капитала. Соотношение капитала/рабочей силы достигает равновесия в долгосрочной перспективе в точке, показанной на рис. 5.3. Это равновесное соотношение связано с уровнем производительности. Единожды достигнутое, оно не нуждается в подпитке капиталом либо рабочей силой со стороны производителя.

Более детальный подход к неоклассической модели роста показывает, что равновесная фондообеспеченность частично определяется производственной функцией и частично другой функцией, связанной с основным уравнением роста.

Эта функция основывается на условии, что капиталовооруженность продолжает расти, пока общая сумма капиталовложений на работника поддерживает необходимый уровень, чтобы заменить изношенное оборудование и увеличить размер капитала, необходимый для роста рабочей силы.

В этой упрощенной версии неоклассической модели не может быть роста дохода на душу населения в долгосрочной перспективе, пока длительное равновесие определяется ситуацией, в которой производительность, капитал и рабочая сила растут одинаковыми темпами.

У роста производительности существуют границы в среднесрочной перспективе, как видно из уравнения

(5.9)

где , это прирост выпуска, – прирост капитала, – прирост рабочей силы.

Константы и показывают доли прироста капитала и затрат труда в приросте выпуска.

Так, если размер капитала вырос на 5% за год, а рабочая сила – на 1%, то темп роста выпуска составит 2,6% при коэффициенте равном 0,4.

Вычленяя AL/L в обеих частях уравнения, можно получить уравнение роста производительности труда:

(5.10)

Из этого уравнения видно, что производительность вырастет на 1,6%, если размер капитала и рабочей силы вырастут на 5% и 1% соответственно.

Но этот рост производительности и дохода на душу населения может проявляться только в среднесрочной перспективе, так как в условиях долгосрочного равновесия капитал и рабочая сила должны расти с одинаковой скоростью.

Можно сделать следующие выводы:

– рост выпуска не имеет границ, пока растут капитал и рабочая сила;

– производительность может вырасти при условии интенсивного увеличения капитала;

– когда фондообеспеченность достигает величины, при которой устанавливается длительное равновесие, дальнейший рост производительности прекращается;

– данную модель можно использовать для анализа регионального развития.