Теория выдвижения и проверки статистических гипотез А. Вальда
Наибольшее распространение из методов принятия статистических решений получил метод, называемый методом выдвижения и проверки гипотез.
Метод возник для оценки процессов передачи сигналов на расстоянии; базируется на общей теории статистических решающих функций А. Вальда; важным частным случаем теории является байесовский подход к исследованию процессов передачи информации, процессов общения, обучения и др. в организационных системах.
Идея метода заключается в следующем.
Имеется два векторных пространства — пространство априорной информации и пространство апостериорной информации. Первое из них иногда называют просто пространством информации 5,; второе — пространством восприятия 5В или пространством решения.
В случае детерминированного (достоверного) восприятия точке х е 5/ соответствует только одна точка х" е 5„.
В случае статистического (вероятностного) восприятия каждой точке .г е 5, соответствует в пространстве 5В распределение (х / х"), которое называется решающей функцией.
Что собой представляет решающая функция, можно пояснить па примере двуальтернативного решения с событиями х, и х и их априорными вероятностями р, И р.
События Х и х в пространстве 5/ могут представлять собой два состояния точки х: хх — отсутствие точки О, х — наличие точки ®.
В пространстве 5И событиям Х и х соответствуют события х{ и х'2 и условные вероятности р(х')/ хх).
Способы восприятия информации приведены на рис. 3.4.

Условные вероятности р(х[/х) и р(х'2/х) характеризуют случаи правильного восприятия:
— р(х / х{) — отсутствие точки х в пространстве восприятия 5В в случае отсутствия ее в пространстве информации 5,;
— р(х'2/х) — обнаружение точки х в пространстве 5В в случае наличия ее в пространстве 5/.
Условная вероятность р(х / хх) характеризует восприятие события х при условии, что в пространстве 5/ произошло событие хь т.е. обнаружение точки х в пространстве 5В в случае ее отсутствия в пространстве 5;. Этот случай называют "ложная тревога".
Условная вероятность р(х{ /х) характеризует отсутствие точки х в пространстве 5„ в случае ее наличия в пространстве 5,. Этот случай называют "пропуск сигнала" (например, самолет появляется, но его не обнаружили).
Для оценки рассмотренных случаев вводится понятие "функция потерь У".
В случае правильного восприятия, т.е. при />(.[ /.{) и р(х/х),

В случае ложной тревоги или пропуска сигнала
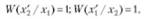
Пользуясь этими оценками потерь, можно ввести понятие условного риска. у
Для случая х{. О—мЭ, а — принятое решение
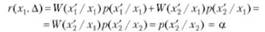
так как У(х{/х,) = 0; Х¥(х/ж,) = 1,
где Д — условный знак, характеризующий возможность отклонения от правильного решения, т.е. условный риск равен вероятности ложной тревоги.

Общий риск (имеют место решения а и Р):

При решении некоторых задач удобнее оперировать не непосредственно с функционалами, а с их отношениями. В частности, с отношением правдоподобия, представляющем собой отношение функционалов правдоподобия условных вероятностей при наличии и при отсутствии сигнала.

Решение о наличии или отсутствии сигнала принимается путем проверки, превышает ли отношение правдоподобия некоторый порог Ь0, т.е. если

то принимается решение о наличии сигнала. В противном случае принимается решение об отсутствии сигнала.
Рассмотренный случай — это критерий Зигерта — Котельникова, называемый часто критерием идеального наблюдения (минимизируется общий риск).
В теории статистических решений используются также следующие критерии:
а) критерий Байеса — критерий минимального риска; ищется минимальный риск из нескольких максимальных общих рисков;
б) критерий минимакса; априорные вероятности неизвестны, и минимизируется значение максимально возможного риска, т.е. ищется ппп Д шах;
в) критерий Неймана — Пирсона; минимизируется (3 при а < е;
г) критерий А. Вальда — последовательный анализ: минимизируется число испытаний п, достаточное для принятия определенного решения. В этом случае производится непрерывный анализ отношения правдоподобия и сравнение его
Р , Иг
с двумя порогами, нижним Ц и верхним ¿2 =~^- если Ь(х) < то принимается решение об отсутствии сигнала; а если Ь(х) > Ь, то принимается решение о наличии сигнала; если же Ьх < Ь(х) < Ь, то имеющихся данных недостаточно для принятия решения и испытания продолжаются.
В рассматриваемом примере пространство априорной информации содержит два события, и решающая функция включает четыре апостериорных условных вероятности с соответствующими им функциями потерь. В случае большего объема событий распределение А(х'/х) усложняется. При выборе решающей функции следует руководствоваться возможностью минимизации среднего риска.
Основы общей теории статистических решающих функций разработаны А. Вальдом. Им же предложен общий подход к постановке задачи принятия статистических решений с интерпретацией ее как антагонистической игры.
Проверка гипотез, теория статистических оценок, вопросы планирования эксперимента могут быть рассмотрены в рамках этой теории как частные случаи.
Независимо от теории решающих функций в теории связи развивалась теория потенциальной помехоустойчивости, начало которой положено работами В. А. Котельникова.
Соединившись в работах Д. Миддлтона, эти два направления образовали теоретико-техническую дисциплину — теорию статистических решений, которая занимается разработкой методов раскрытия неопределенности пространства апостериорной информации.