Связь между ARIMA и экспоненциальным сглаживанием
Между моделями ARIMA, рассмотренными нами в данной главе, и моделями экспоненциального сглаживания, рассмотренными нами η гл. 7, существует связь. Одно время статистики, обратив внимание на то, что многие модели экспоненциального сглаживания являются частными случаями моделей ARIMA, пришли к выводу о том, что первые и вовсе не нужны. Однако это заключение впоследствии было признано ошибочным[1] по следующим причинам:
1. Не все модели ETS имеют аналоги в моделях ARIMA. Например, нелинейные модели экспоненциального сглаживания (с мультипликативной ошибкой, трендом или сезонностью) не имеют аналогов среди моделей ARIMA.
2. Модели экспоненциального сглаживания строятся, исходя из конечных стартовых значений, а модели ARIMA предполагают, что временно́й ряд имеет бесконечное прошлое.
3. Все модели ARIMA стационарны, так как этого требует методология Бокса – Дженкинса, в то время как практически все модели экспоненциального сглаживания по сути своей нестационарны.
4. Эти два разных класса моделей основаны на совершенно разных подходах, которые дают соответственно разные результаты при прогнозировании.
Тем не менее модели связаны друг с другом, и выражение моделей экспоненциального сглаживания через модели ARIMA может быть полезным, так как позволяет по-другому взглянуть на эти модели.
Покажем на нескольких примерах эту связь. Удобнее всего выявлять ее на моделях в форме коррекции ошибок, представленных в табл. 7.6.
Для начала рассмотрим простейшую модель – модель Брауна, ETS(A,N,N). Напомним ее математическую формулу:
Приводя модель (8.76) к "уменьшенному виду", т.е. к виду одного уравнения, получим
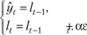(8.76)
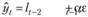(8.77)
Далее, используя первое равенство в системе (8.76), заменим lt-1 в (8.77):
Затем заменим расчетные значения на фактические с ошибками:
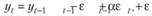
Перенесем yt в левую часть и сгруппируем ошибки в правой. Получим
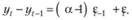(8.78)
Если теперь в левой части (8.78) ввести разностный оператор, а (α – 1) заменить на коэффициент c1, то мы получим модель
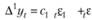или
. (8.79)
Перед нами модель ARIMA(0,1,1). Используя модель (8.79), можно не только произвести оценку коэффициента при помощи стандартного подхода, но, например, еще и вывести ограничения на постоянную сглаживания а. Так, для выполнения свойства обратимости модели для модели МА(1) должно выполняться условие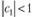 
, которое соответствует условию 
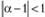, из которого, в свою очередь, следует знакомое нам условие 0 < α < 2.
Стоит отдельно отметить, что в случае, когда α = 0, модель Брауна еще имеет какой-то смысл (ряд данных описывается стартовым значением, в качестве которого может выступать, например, средняя величина), а вот в модели МА(1) эквивалентное ему условие c1 = 1 уже неприемлемо, так как в таком случае модель теряет свойство обратимости.
Рассмотрим для примера еще одну модель – модель Хольта, ETS(A,A,N), которая описывается системой уравнений:
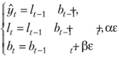(8.80)
Первое уравнение в системе (8.80) может быть переписано через фактическое значение с ошибкой:
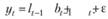(8.81)
Подставим второе и третье уравнения в первое в (8.80), а также подставим вместо расчетного значения (8.81):
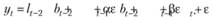
Используя (8.81), заменим сумму уровня с коэффициентом прироста:
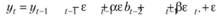(8.82)
Теперь выразим из (8.81) bt-1 и подставим его в (8.82):
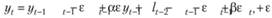
заменим значение /t_2 на значение из второго уравнения в (8.80), попутно используя (8.81):
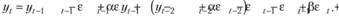(8.83)
Теперь перегруппируем значения в (8.83) так, чтобы все yt находились в левой части, а все ошибки – в правой:
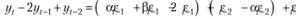
и вынесем все одинаковые ошибки за скобки:
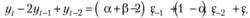(8.84)
В левой части (8.84) представлено не что иное, как вторая разность по уt, которую мы обычно записывали следующим образом:
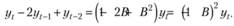(8.85)
Подставляя (8.85) в (8.84) и переходя к лаговым операторам, придем к финальной формуле:
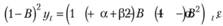(8.86)
Если в этой формуле заменить (α+β-2) на c1, а (l-α) на с2, то мы придем к модели АRIМА(0,2,2):
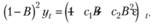
Из этой же модели, в свою очередь, можно получить ограничения на постоянные сглаживания (7.67) в модели Хольта.
По аналогии с этими двумя примерами можно показать, что многие другие модели экспоненциального сглаживания имеют аналоги среди моделей ARIMA. В частности:
1) ETS(A,Ad,N) эквивалентна ARIMA( 1,1,2);
2) ETS(A,N,A) эквивалентна SARlMA(0,0,s) × (0,1,0)s;
3) ETS(A,A,A) эквивалентна SARIMA(0,l,s+1) × (0,1,0)s;
4) ETS(A,Ad,A) эквивалентна SARIMA(l,0,s+l) × (0,1,0)s.
Мультипликативные модели ETS аналогов среди ARIMA не имеют.