Структура турбулентного потока

Рассмотрим турбулентный поток в трубе круглого сечения (рис. 6.13).

Очевидно, что на стенке трубы возникновение поперечных пульсаций невозможно. Поэтому вблизи самой стенки парализуется возможность перемешивания. Это дает основание предполагать, что на некотором расстоянии от стенки должен быть расположен весьма тонкий ламинарный слой, так называемая ламинарная пленка некоторой толщины Опыты вполне подтверждают это предположение.

Рис. в.13. Структура турбулентного потока:

1 – турбулентное ядро; 2 – ламинарный гидродинамический пограничный слой

Таким образом, турбулентный поток в трубе можно представить схематично состоящим по меньшей мере из двух составляющих (двухслойная модель турбулентного потока): ядра потока с турбулентным движением (турбулентное ядро) и ламинарного гидродинамического пограничного слоя (ламинарная пленка), имеющего толщину .

В пределах ламинарной пленки скорость существенно изменяется от нуля до значенияна границе с турбулентным ядром. Далее из-за перемешивания жидкости скорость изменяется медленнее.

Произведем оценку толщины ламинарной пленки Касательное напряжение на стенке

Так как , то

Величину

имеющую размерность скорости (м/с), принято называть динамической скоростью или скоростью касательного напряжения у стенки. Динамическая скорость является одной из важнейших характеристик турбулентного потока, и для данного потока она является постоянной величиной.

Динамическая скорость и является расчетной характеристикой и особого физического смысла не имеет. Она составлена по аналогии с обычным приемом, принятым в аэродинамике, – характеризовать скорость набегающего потока динамическим давлением:

, или

Учитывая, что 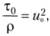можно записать

или

Левая часть последнего уравнения конструктивно сходственна с числом Рейнольдса. По аналогии с переходом потока от ламинарного режима к турбулентному, характеризуемому числом Рейнольдса, можно предположить, что переход от ламинарной пленки к турбулентному ядру происходит также всегда при одном и том же значении комплекса

Отсюда можно записать

По опытам И. Никурадзе, это число оказалось равным N=11. Отсюда найдем:

,

где

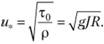
Касательные напряжения в турбулентном потоке

При исследовании закономерностей турбулентного течения в трубах целесообразно исходить из выражений для касательных напряжений. Их природа в турбулентном потоке более сложна, чем в ламинарном. Это связано с тем, что в процессе турбулентного перемешивания массы жидкости из центральной части трубы могут попасть в область потока у стенок, и наоборот.

Массы жидкости, перемещающиеся из центральной части трубы к периферийной, обладают большими продольными скоростями, чем двигающиеся в обратном направлении. Такой обмен массами жидкости, имеющими разные скорости, приводит к соответствующему обмену количеством движения.

Рассмотрим простейший случай осредненного турбулентного потока (рис. 6.14). В целях упрощения записи формул введем следующие обозначения:

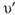где и – пульсации скоростей соответственно по осям х и у.

Так как поток принят плоскопараллельным, то, очевидно,

Покажем, что в таком потоке будет возникать дополнительное касательное инерционное напряжение, равное

,

где – осредненное значение произведения пульсаций скорости

Рассмотрим два соседних слоя жидкости, разделенных площадкой . Пусть вблизи верхней поверхности площадки имеют место пульсации скоростей и . В этом случае можно сказать, что верхний слой жидкости движется относительно нижнего с какой-то относительной скоростью .

Под действием вертикальной пульсации скорости через площадку за время протечет масса жидкости

Рис. 6.14. Схема скоростей и напряжений в осредненном турбулентном потоке

В верхнем слое эта масса получит ускорение в направлении оси х. При ускорении этой массы верхним слоем на нижнюю часть последнего будет действовать сила инерции, направленная в сторону, обратную ускорению, т.е. жидкость, поступающая из нижнего слоя в верхний, будет затормаживать его. Этот эффект торможения равносилен приложению к верхнему слою на поверхности раздела слоев по площадке Δω некоторой касательной силы инерции ΔТ, направленной противоположно движению, или касательного напряжения т (на нижний слой по третьему закону Ньютона будет действовать напряжение т в сторону движения). Касательную силу ΔТ легко подсчитать.

Изменение количества движения жидкости, перешедшей из нижнего слоя в верхний, будет

Это изменение количества движения равно импульсу касательной силы ΔТ, т.е.

Знак "минус" поставлен потому, что сила инерции всегда направлена против ускорения.

Учитывая, что

получаем

или осредненное за период Т

Это и есть выражение для турбулентного касательного напряжения в функции от пульсационных скоростей.

Полное напряжение в турбулентном потоке определится по формуле

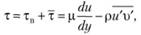(6.11)

где – касательное напряжение, от действия сил вязкости; – напряжение, обусловленное турбулентным перемешиванием.

При ламинарном движении перемешивания не происходит и в формуле (6.11)