Статистический инструментарий в маркетинговом анализе

Маркетинговый анализ активно использует статистический инструментарий. Основные причины этого следующие:

• потребность в применении многомерного анализа;

• необходимость на основании выборочных исследований делать выводы по генеральной совокупности. Выборка должна быть репрезентативна, или должны применяться специальные статистические методы для повышения ее репрезентативности;

• исследование случайных переменных, т.е. переменных, содержащих случайную компоненту.

В зависимости от целей и задач маркетингового анализа применяются различные методы математической статистики и эконометрики (табл. 7.16).

Таблица 7.16. Виды статистического анализа, применяемые для решения маркетинговых задач

Цель маркетинга	Виды статистического анализа			Задачи управления по результатам анализа
Прогнозирование рыночных тенденций и спроса	Методы прогнозирования временных рядов: • тренд-сезонная модель; • адаптивные методы прогнозирования			Корректировка стратегии и тактики маркетинга в зависимости от рыночной ситуации. Разработка маркетингового бюджета компании
Сегментирование рынка		• кластерный анализ; • дискриминантный анализ; • деревья классификации	Выбор сегментов для дальнейшего развития, выход на новые сегменты
Анализ потребительских предпочтений		• факторный анализ; • анализ; • карты восприятия: — анализ соответствии, — многомерное шкалирование; • связь показателей: — корреляционный анализ; — регрессионный анализ	Позиционирование компании и ее продуктов, оценка концепций новых продуктов, разработка характеристик продуктов в соответствии с требованиями потребителей

Кластерный анализ — используется для сегментирования рынка па основании естественных группировок потребительских предпочтений.

Факторный анализ — позволяет оценивать потребительские предпочтения, выявлять взаимосвязь показателей. Может использоваться для построения карт восприятия.

Дискриминантный анализ — относится к методам сегментации с откликом. На основании имеющихся данных позволяет построить дискриминантную функцию для классификации объектов (например, на основании демографических признаков, потребителей, которые приобретут продукцию компании с достаточно высокой вероятностью).

Деревья классификации — позволяют сформулировать правило классификации объектов в зависимости от значительного числа категориальных факторов. Метод, как и дискриминантный анализ, относится к сегментации с откликом.

Conjoint-анализ — используется для оценки потребительских предпочтений. Применяется для оценки привлекательности маркетинговых концепций новых товаров.

Для построения карт восприятия, необходимых для позиционирования товаров, применяются факторный анализ, анализ соответствий и многомерное шкалирование.

В целях формирования общего представления об исходных данных применяется первичный анализ, включающий описательные статистики и графический анализ.

В маркетинговом анализе исследуются различные переменные — это то, что можно измерять, контролировать или изменять. Переменные отличаются многими аспектами, особенно той ролью, которую они играют в исследованиях, шкалой измерения и т.д.

Фактором, определяющим количество информации, содержащейся в переменной, является тип шкалы, в которой проведено измерение. Различают следующие типы шкал: номинальная, порядковая (ординальная), количественная. Соответственно, существует три основных типа переменных: поминальная, порядковая (ординальная), и количественная. Номинальные и порядковые переменные называются категориальными.

Номинальные переменные используются только для качественной классификации. Данные переменные могут быть измерены только в терминах принадлежности к некоторым, существенно различным классам; при этом нельзя определить количество или упорядочить эти классы. Типичные примеры номинальных переменных — пол, национальность, цвет, город и т.д.

Порядковые переменные позволяют ранжировать (упорядочить) объекты, указав, какие из них в большей или меньшей степени обладают качеством, выраженным данной переменной. Однако они не позволяют сказать "насколько больше" или "насколько меньше". Порядковые переменные иногда также называют ординальными. Типичный пример порядковой переменной — уровень дохода или образования.

Количественные переменные позволяют не только упорядочивать объекты измерения, но и численно выразить и сравнить различия между ними. Например, цена товара, объем продаж, уровень дохода человека в денежном выражении.

В качестве описательных статистик для количественных переменных можно использовать среднее, медиану и среднее квадратическое отклонение. Для порядковых — медиану и моду, для номинальных — только моду.

Для представления категориальных переменных в статистических программах используют их кодировку. Рассмотрим примеры кодировок. Пол: мужчины — 0, женщины — 1; уровень образования: среднее — 1, высшее — 2, ученая степень — 3.

Переменные подразделяются на зависимые и независимые. Зависимость переменных проявляется в ответной реакции исследуемого объекта на посланное на него воздействие. Например, в большинстве случаев цена является независимой переменной, в то время как объем продаж — зависимой.

В процессе анализа информации исследователи сталкиваются с проблемой пропущенных значений, которые могут быть двух типов: системные — отсутствуют данные, и пользовательские — описанные в кодировке. Например, на вопрос "Оцените качество обслуживания" предусматривается трехбалльная шкала: 1 — низкое, 2 — среднее, 3 — высокое, 7 — пет ответа. 7 — это пользовательское пропущенное значение

Для повторяющихся значений и повышения репрезентативности выборки используется взвешивание данных. В том случае, если пропорции в выборочной совокупности по результирующему количественному или категориальному признаку не соответствуют данным по генеральной совокупности, за счет введения поправочных весовых коэффициентов можно повысить репрезентативность выборки.

Часто в маркетинговых данных одновременно присутствуют как категориальные, так и количественные переменные. Первичный анализ может быть связан с исследованием каждой из переменных или их взаимосвязи.

Рассмотрим категориальные переменные. По ним можно построить частотную таблицу, показывающую число наблюдений, относящихся к гой или иной категории переменной, а также вывести столбиковую и круговую диаграмму (по числу наблюдений, с выведением процентов для столбиковой диаграммы).

По количественным переменным можно вывести описательные статистики (среднее, среднее квадратическое отклонение и др.), квартили, процентили и гистограмму. Меню в SPSS: анализ — описательные статистики — описательные, анализ — описательные статистики — частоты.

В целях выявления связей между переменными применяются таблицы сопряженности. Кросстабуляция — это процесс объединения двух (или нескольких) таблиц частот так, что каждая ячейка (клетка) в построенной таблице представляется единственной комбинацией значений или уровней табулированных переменных. Таким образом, кросстабуляция позволяет совместить частоты появления наблюдений на разных уровнях рассматриваемых факторов. Исследуя эти частоты, можно определить связи между табулированными переменными. Обычно табулируются категориальные (номинальные) переменные или переменные с относительно небольшим числом значений. Полученные в результате кросстабуляции таблицы называют таблицами сопряженности.

Если для построения таблиц использовались две переменные, такая таблица называется двухвходовой. Критерий Хи-квадрат Пирсона представляет собой наиболее простой критерий проверки значимости связи между двумя категоризованными переменными. Критерий Пирсона основывается на том, что в двухвходовой таблице ожидаемые частоты при гипотезе "между переменными нет зависимости" можно вычистить непосредственно. Например, оценка связи между предпочтением различных марок товара и полом. Если между предпочтением и полом нет связи, то естественно ожидать равного выбора между марками для каждого пола.

Часто возникает задача сравнения средних значений различных категорий наблюдений. Например, различается ли средний чек в магазинах различных торговых сетей. Для визуализации средних удобно использовать столбиковую диаграмму.

Для обнаружения различия между средними двух выборок применяется г-критерий, как наиболее часто используемый метод. Теоретический критерий может применяться, даже если размеры выборок очень небольшие (например, 10) и если переменные нормально распределены (внутри групп), а дисперсии наблюдений в группах не слишком различны. Уровень значимости ^-критерия равен вероятности ошибочно отвергнуть гипотезу о равенстве средних двух выборок, когда в действительности эта гипотеза имеет место. Иными словами, он равен вероятности ошибки принять гипотезу о неравенстве средних, когда в действительности средние равны.

Если необходимо сравнить средние значения более двух категорий, необходимо применять однофакторный дисперсионный анализ. Основной целью дисперсионного анализа является исследование значимости различия между средними. Если просто сравнивать средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный ^-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или г- критерий для зависимых выборок (сети сравниваются две переменные на одном и том же множестве объектов или наблюдений). Проверка значимости в дисперсионном анализе основана на сравнении компоненты дисперсии, обусловленной межгрупповым разбросом. Если верна нулевая гипотеза, то можно ожидать сравнительно небольшое различие выборочных средних из-за чисто случайной изменчивости. Поэтому при пулевой гипотезе виутригрупповая дисперсия будет практически совпадать с общей дисперсией, подсчитанной без учета групповой принадлежности. Полученные внутригрупповые дисперсии можно сравнить с помощью ^-критерия, проверяющего, действительно ли отношение дисперсий значимо больше 1.

Создание диаграмм позволяет визуализировать исходные данные. Круговую и столбиковую диаграмму удобно использовать для анализа частот, в том числе и по кластерам (группам). Диаграмма рассеяния позволяет дать в первом приближении оценку связи между двумя количественными переменными, на график можно вывести аппроксимирующие линии, в том числе и по подгруппам.

Коробчатая диаграмма (ящичная, диаграмма размаха): используется для сравнения медиан, представленных точками, прямоугольник представляет диапазон от 1-го до 3-го квартиля, "усы" — максимальные и минимальные значения, если они не являются выбросами. Экстремальные значения, удаленные более чем на 3 длины прямоугольника, помечаются звездочками, на 1,5 длины — кружочками.

Гистограммы являются графическими представлениями распределения частот выбранных переменных, на которых для каждого интервала (категории) рисуется столбец, высота которого пропорциональна частоте категории (рис. 7.7).

Диаграмма рассеяния визуализирует зависимость между двумя переменными X и У (например, ценой и объемом продаж). Данные изображаются точками в двухмерном пространстве, где оси соответствуют переменным (X — горизонтальной, а У — вертикальной оси). Зависимая переменная соответствует вертикальной оси К (рис. 7.8).

Матричные графики рассеяния (рис. 7.9): на матричном графике этого типа изображаются двухмерные диаграммы рассеяния, организованные в форме матрицы (значения переменной по столбцу используются в качестве координат X, а значения переменной по строке — в качестве координат У). Гистограммы, изображающие распределение каждой переменной, располагаются на диагонали матрицы (в случае квадратных матриц) или по краям (в случае прямоугольных матриц).

Рис. 7.7. Гистограмма показателя вложения в недвижимость банками

Рис. 7.8. Диаграмма рассеяния по активам и капиталу банков

Рис. 7.9. Матричная диаграмма рассеяния по показателям деятельности банков

Рис. 7.10. Столбчатая диаграмма активов и капитала банков

Столбчатая диаграмма (рис. 7.10): на этой диаграмме для каждой точки данных (т.е. для каждой пары координат ХУ) рисуется один вертикальный столбец, соединенный с нижней осью X. Горизонтальное положение столбца определяется координатой X точки данных, а его высота — соответствующим значением переменной У.

На линейных графиках отдельные точки данных соединены линией. Эти графики являются простым способом представления и исследования последовательностей значений, например временных рядов (рис. 7.11).

Круговые диаграммы: на этих графиках пропорции отдельных значений переменной X представлены в виде круговых секторов (рис. 7.12).

Существуют и другие графики для визуализации исходных данных.

К методам, позволяющим оценить степень взаимосвязи показателей между количественными переменными, относятся корреляционный и регрессионный анализ.

Рис. 7.11. Изменение во времени показателей биржевой деятельности

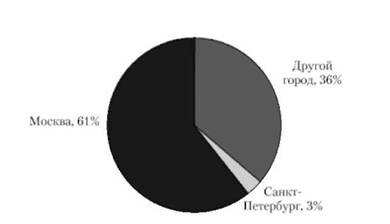
Рис. 7.12. Доли банков различных городов но количеству в выборке

Одним из наиболее часто применяемых показателей взаимозависимости двух случайных количественных величин является парный коэффициент корреляции. Он является мерой линейной статистической зависимости между двумя величинами. Выборочный коэффициент корреляции г, как всякая выборочная характеристика, является случайной величиной, и по отдельным его значениям нельзя делать окончательные выводы о степени тесноты линейной связи между двумя величинами. Речь может идти о некоторых практических, качественных рекомендациях при достаточно больших объемах выборки п > 40. Для определения силы взаимосвязи можно воспользоваться табл. 7.17.

Таблица 7.17. Оценка силы связи между двумя переменными с помощью коэффициента корреляции

После того как с помощью корреляционного анализа выявлено наличие статистических связей между переменными и оценена степень их тесноты, обычно переходят к математическому описанию конкретного вида зависимостей с использованием регрессионного анализа. С этой целью подбирают класс функций, связывающий результативный показатель у и аргументы х]у хъ ... , хк, отбирают наиболее информативные аргументы, вычисляют оценки неизвестных значений параметров уравнения связи и анализируют свойства полученного уравнения.

Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Например, агент по продаже недвижимости мог бы вносить в каждый элемент реестра размер дома (в квадратных метрах), число спален, средний доход населения в этом районе в соответствии с данными переписи и субъективную оценку привлекательности дома. Как только эта информация собрана для различных домов, было бы интересно посмотреть, связаны ли и каким образом эти характеристики дома с ценой, по которой он был продан. Например, могло бы оказаться, что число спальных комнат является лучшим предсказывающим фактором (регрессором, предиктором) для цепы продажи дома в некотором специфическом районе, чем "привлекательность" дома (субъективная оценка). Могли бы также обнаружиться и "выбросы", т.е. дома, которые могли бы быть проданы дороже, учитывая их расположение и характеристики.

Результатом регрессионного анализа является модель, представленная уравнением регрессии. Мерой адекватности модели исходным данным служит мера согласия — коэффициент детерминации — І?2 и характеристики остатков.

Инструментом сегментации рынка выступает многомерная классификация. Рассмотрим статистические методы многомерной классификации, применяемой для сегментации рынка (рис. 7.13).

Рис. 7.13. Методы сегментации рынка

Кластерный анализ — это один из методов разведочного анализа данных, созданных для выявления естественных группировок в совокупности данных. В этом смысле кластерный анализ может потенциально оказаться полезным способом при группировке потребителей. Кластерный анализ был опробован на различных классах маркетинговых данных: психографике, поведении, рейтингах товаров, информации об использовании и осознании преимуществ, В основе кластерного анализа лежит простая концепция распределения наблюдаемых данных по однородным группам в зависимости от их сходства (близости) друг с другом.

Факторный анализ — это статистическая техника разведочного анализа данных, часто используемая как метод сокращения размерности данных. Факторный анализ предлагает способы сокращения числа имеющихся переменных в меньший набор составных переменных, которые аккумулируют большую (по крайней мере, в идеале) часть информации, содержащуюся в исходном наборе данных. При проведении сегментации рынка этот метод используется для сжатия данных перед кластеризацией в ситуациях, когда имеется много переменных, которые могут быть потенциально использованы в кластерном анализе, и (или) когда исследователь ожидает некоторую избыточность среди кластерных переменных. Новые составные переменные, созданные при проведении факторного анализа (их называют факторизованными), используют затем как основу для кластеризации.

Сегментация рынка, основанная на откликах — это общее понятие, охватывающее различные методы, которыми пытаются определить, какая комбинация характеристик потребителя приводит к определенному действию (приобретению, обновлению, замене). В этом смысле эти методы являются прогностическими и дают в результате либо уравнение, либо набор описаний, полезных при определении потребителей, попадающих в желаемую группу.

Дискриминантный анализ и логистическая регрессия — это прогностические модели, в которых результирующий показатель (отклик) является категориальным (купил / не купил), а независимые переменные измерены в интервальной (числовой) шкале. Как и в регрессионном анализе, основная идея здесь — построить прогностическую модель, оценить ее и в случае успеха создать соответствующее уравнение. На практике оба метода дают схожие результаты, хотя для дискриминантного анализа требуются более строгие предположения относительно природы независимых переменных.

Деревья классификации дают эвристический метод изучения сразу многих независимых переменных для определения таких комбинаций категорий, которые дают наивысший процент при желаемом условии отклика. Данная статистическая техника часто используется в исследованиях методом прямой почтовой рассылки при выявлении демографии тех, кто с наибольшей вероятностью приобретет предложенный товар.

Для оценки потребительских предпочтений наиболее популярными являются следующие статистические методы:

• совместный анализ;

• анализ соответствий;

• многомерное шкалирование.

Эти методы, как правило, базируются па достаточно специфичных мерах (ранги или рейтинги гипотетических товаров, суждения о сходствах или различиях реальных товаров). Обычно уже на этапе планирования исследования и сбора данных принимается во внимание, что анализ будет проводиться с использованием этих методов, хотя существуют исключения, и в некоторых случаях рассматриваемые методы применяются для анализа уже собранных данных.

Совместный анализ (conjoint) широко используется при разработке новых товаров или услуг. Он обеспечивает получение информации относительно восприятия и осуществления выбора между различными характеристиками (атрибутами) товара (услуги). Предметом conjoint-анализа обычно являются результаты ранжирования, выставления оценок или выбора одного варианта товара из нескольких описаний. Описание товара дается в терминах его атрибутов или характеристик (например, цена, цвет, вес) и иногда сопровождается графическим изображением. Предъявляемые варианты товара являются сбалансированным набором комбинаций атрибутов, так что каждый из уровней атрибута появляется в сочетании с другими уровнями других атрибутов. Таким образом, респонденты оценивают не два или три возможных варианта товара, а полный диапазон атрибутов. Это обеспечивает получение информации, необходимой для оценки относительной важности каждого атрибута товара и определения наиболее предпочтительной комбинации атрибутов. Поскольку для анализа необходимо получить ранги, оценки или результаты выбора из нескольких вариантов товара, то данные для такого анализа собираются путем интервьюирования или с использованием специального программного обеспечения. В то же время информацию можно получать с использованием инструментов проведения обследований.

В качестве примеров проведения анализа можно привести следующие:

• оценка новых лекарств или медицинского оборудования в отношении их эффективности, побочных эффектов, свойств и стоимости с точки зрения потребителя;

• оценка того, какие качества нового снегохода, автомобиля или программного продукта являются наиболее важными для потребителя;

• оценка суждений относительно стоимости и свойств технической поддержки (время, уровень компетентности, варианты связи).

Карты восприятия (или перцептивные карты) — это способ графического представления информации в сочетании со статистическими методами визуализации взаимосвязей и различий в данных. Этот метод предполагает построение диаграмм в соответствии с баллами переменных или категорий переменных для индивидуальных объектов или групп объектов в пространстве, полученном в результате выполнения специального статистического анализа. Он может использоваться для оценки относительного расположения товаров или групп потребителей в пространстве малой размерности (чаще всего в двухмерном пространстве). Для построения карт восприятия широко применяется анализ соответствий. Анализ соответствий применим к двух-входовым или многовходовым таблицам сопряженности, содержащим встречаемости (например, таблица групп потребителей по видам товаров, которые они предпочитают).

За счет применения другой меры расстояния этот метод может быть применен также к таблицам, содержащим средние значения (например, таблица, в строках которой содержатся средние оценки товара по различным атрибутам, а столбцы определяются марками товара). Оценивается при этом взаимное расположение марок товара в зависимости от их оценок потребителями в рейтинговой шкале.

Примеры карт восприятия включают:

• расположение марок товара в пространстве малой размерности в соответствии с оценками их качеств;

• покупаемые товары располагаются в одном пространстве с группами потребителей (подразделениями предприятий, демографическими группами или странами);

• виды предложений или жалоб располагаются в одном пространстве с различными продуктами или демографическими группами.

Многомерное шкалирование представляет собой метод представления объектов в пространстве малой размерности на основе мер близости (различия) между объектами. Практическое отличие многомерного шкалирования от карт восприятия заключается в используемых исходных данных (в многомерном шкалировании обычно используются меры различия, а не встречаемости или средние оценки, хотя существуют и исключения), а также в некоторых технических аспектах шкалирования. Обычно многомерное шкалирование включает анализ оценок различий (уже имеющихся или вычисляемых но данным) объектов (например, марок товара или кандидатов на выборах) и отображение объектов в пространстве меньшей размерности для понимания относительно расположения объектов и измерений, учитывающих различия.

Существует множество видов многомерного шкалирования, различающихся, в частности, исходными предположениями относительно шкалы измерения, возможными преобразованиями, средствами учета индивидуальных различий и методом оценки согласия модели. Далее будут рассмотрены несколько наиболее распространенных форм многомерного шкалирования.

Примеры многомерного шкалирования:

• позиционирование напитков, автомобилей или журналов в пространстве, определяемом оценками близости объектов;

• позиционирование марок товара по данным о различиях, рассчитанным но оценкам нескольких атрибутов;

• позиционирование товаров и расчет отдельных идеальных точек на основе рангов или рейтингов товаров.

Для разработки маркетингового бюджета компании, проведения аудита с целью корректировки стратегии компании строится прогноз спроса на продукцию фирмы. Для решения этих задач необходимо построение помесячного прогноза товарооборота (дохода) на год. Для построения прогноза используется временной ряд товарооборота за предшествующие периоды деятельности компании. Поскольку в данном ряде практически всегда присутствует сезонная компонента, а период сезонных колебаний — 12 месяцев, для корректного учета сезонности необходимо иметь временной ряд длиной не менее трех лет.

Еще одной проблемой прогнозирования ряда товарооборота является его изменчивость с течением времени. Изменение маркетинговой политики, усиление влияние одних экономических факторов и ослабление влияния других приводит к нестабильности ряда. Последние зафиксированные уровни ряда являются значительно более значимыми, чем предыдущие. Таким образом, влияние на прогнозируемые уровни в большей степени оказывают последние наблюдения. В этой связи для анализа временных рядов целесообразно использовать адаптивные методы прогнозирования, такие как экспоненциальное сглаживание и модель авторегрессии и проинтегрированного скользящего среднего (АШМА) Бокса-Дженкинса. Адаптивные методы прогнозирования взвешивают исходные данные и придают наибольший вес последним наблюдениям.

Сезонная декомпозиция позволяет разделить временной ряд (Х[у где I — момент времени) на ряд компонент;

1) сезонной компоненты (5,);

2) тренд-циклической компоненты, включающую тренд и циклическую компоненту (Та);

3) случайной, нерегулярной компоненты (£,). Разница между циклической и сезонной компонентой состоит в том, что последняя имеет регулярную (сезонную) периодичность, тогда как циклические факторы обычно имеют более длительный эффект, который к тому же меняется от цикла к циклу. Конкретные функциональные взаимосвязи между этими компонентами могут иметь различный вид. Однако можно выделить два основных способа, с помощью которых они могут взаимодействовать: аддитивно и мультипликативно:

• аддитивная модель: Хг = Та + 5, + Е,

• мультипликативная модель: Х( = Т( х С1 х 5, х Е,.

По своей природе сезонная компонента может быть аддитивной или мультипликативной.

Экспоненциальное сглаживание является очень популярным методом прогнозирования многих временных рядов.

Рассмотрим принципы данного метода на примере простого экспоненциального сглаживания. Простое экспоненциальное сглаживание применяется в том случае, если модель временного ряда имеет следующий вид:

Х,=Ь+Еп

где Ь — константа; Е( — случайная ошибка. Константа Ь относительно стабильна на каждом временном интервале, по может также медленно изменяться со временем. Один из интуитивно ясных способов выделения /; состоит в том, чтобы использовать сглаживание скользящим средним, в котором последним наблюдениям приписываются большие веса, чем предпоследним, предпоследним большие веса, чем предпредпоследним и т.д. Более старым наблюдениям приписываются экспоненциально убывающие веса, при этом, в отличие от скользящего среднего, учитываются все предшествующие наблюдения ряда, а не те, что попали в определенное окно. Точная формула простого экспоненциального сглаживания имеет следующий вид:

5, = ахХ, + (1 -а)*5(г- 1).

Когда эта формула применяется рекурсивно, то каждое новое сглаженное значение (которое является также прогнозом) вычисляется как взвешенное среднее текущего наблюдения и сглаженного ряда. Очевидно, результат сглаживания зависит от параметра а, которое если равно 1, то предыдущие наблюдения полностью игнорируются. Если равно 0, то игнорируются текущие наблюдения. Значения между 0 и 1 дают промежуточные результаты.

В более сложных моделях экспоненциального сглаживания учитываются влияние аддитивной или мультипликативной сезонности и линейного или нелинейного тренда.

Модель АRIМА — АРПСС. Авторегрессии и проинтегрированное скользящее среднее относится к адаптивным методам прогнозирования, которые позволяют строить самокорректирующие экономико-математические модели. Эти модели способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда. Информационная ценность последних наблюдений в экономических рядах обычно значительно выше, чем более ранних, так как информация очень быстро теряет свою актуальность в силу высокой турбулентности экономической среды.

Большинство наблюдаемых моделей стационарных рядов (без учета тенденции и сезонности) может быть отнесено с высокой степенью точности к одному из пяти классов:

1) модели авторегрессии с одним параметром: р = 1, # = 0;

2) модели авторегрессии с двумя параметрами: р = %ц = 0;

3) модели скользящего среднего с одним параметром:/) = 0, д-1;

4) модели скользящего среднего с двумя параметрами: Р = 0,д = 2;

5) модели авторегрессии с одним параметром и скользящего среднего с одним параметром: р = 1, # = 1.

Параметры модели подбираются эмпирически, качество различных моделей сравнивается по характеристикам остатков — разности смоделированных и фактических значений. В хорошей модели взаимосвязь остатков низкая, графики автокорреляционной и частной автокорреляционной функции не превышают допустимых границ.

Для сезонных моделей AРПСС сезонные параметры Р и <2 могут быть определены для каждого из вышеперечисленных классов моделей.

Изменение переменных до обработки позволяет приблизить временной ряд к стационарному состоянию. Наиболее часто используются:

• разность с соответствующим лагом — для исключения полиномиального тренда;

• натуральное логарифмирование — для исключения экспоненциального тренда;

• возведение в соответствующую степень — для исключения логарифмического тренда.

Рассмотренные методы маркетингового анализа позволяют составить полное представление о положении компании на рынке, оценить ее позицию по отношению к конкурентам, а также проанализировать восприятие ее товаров потребителями, что вкупе с комплексом информации о внутренней среде компании позволит принять правильные стратегические решения по дальнейшему развитию компании.