Статистические методы анализа применительно к лонгитюдным данным

Сложность, характеризующая лонгитюдный метод как группу исследовательских схем, в полной мере распространяется на статистический анализ получаемых лонгитюдных данных. Нормативы такого анализа претерпели существенные изменения в последние десятилетия, существенно расширив доступные психологу альтернативы. Выбор аналитических стратегий зависит как от лонгитюдного дизайна (количества временных срезов и их временной удаленности) и проверяемых в нем гипотез, так и от уровня статистической подготовки самого исследователя.

Различают три основные области применения лонгитюда, из которых в контексте построения учебника особо интересуют две основные: 1) экспериментальные и квазиэкспериментальные исследования, 2) исследования роста и развития. В первом случае исследователя интересуют преимущественно кратковременные изменения и различия в них между экспериментальной и контрольной группами после осуществления воздействия. Во втором случае выявляются долгосрочные паттерны изменений и их систематические связи с различными характеристиками испытуемых.

Дизайн исследования включает планирование размера выборки, и два указанных типа исследований различаются и по этому параметру (большие п в первом и меньшие — во втором случае), что также регулирует выбор методов анализа. Так, для больших выборок и большого количества срезов наиболее информативны многомерные модели кривых развития (multilevel growth curve models), а для маленьких выборок и большого количества срезов — ауторегрессионный анализ временных серий (autoregressive lime series models).

В современных работах [Menard, 2008; Singer, Willett, 2003] даются подробные описания указанных и других методов анализа. Остановимся только на критических различиях между "классическим" для отечественных лонгитюдных исследований подходом — использованием ANOVA для повторяющихся измерений (repeatedmeasures ANOVA) — и современными методами. К ним относятся в первую очередь иерархическое линейное моделирование (hierarchical linear modeling, HLM, аналогично multilevel growth cuwe modeling) и моделирование изменений латентных переменных в рамках структурного моделирования, или моделирования на основе структурных уравнений (latentgrowth cuwe modeling; structural equation modeling, SEM). Оба подхода описаны в предыдущих главах.

Наиболее часто используемый метод анализа лонгитюдных данных, ANOVA для повторяющихся измерений, входит в класс общих линейных моделей (general linear models, GLM), основной целью которых является выявление межгрупповых различий в средних изменяющихся со временем показателей. Использование GLM в лонгитюдных исследованиях ограничивается частотой нарушений статистических требований GLM, например, независимости и гомогенности остатков (так называемая проблема сферичности, sphericity), что ведет к искажениям при проверке статистических гипотез с помощью этого метода. Другим ограничением этого метода является невозможность квантификации интраиндивидуальных изменений показателей, неприспособленность этого метода к использованию недихотомических факторов и предикторов, сложности в преодолении проблемы пропущенных данных и невозможность построения истинно нелинейных моделей (включающих экспоненты).

Большая часть из этих ограничений снимается при использовании двух связанных групп методов, являющихся современным вариантом развития регрессионного анализа, а именно методов иерархического линейного моделирования ULM и структурного моделирования SEM. Оба метода позволяют моделировать сложные кривые развития путем установления соответствия данных гипотетическим моделям роста. Кратко опишем эти методы.

HLM предполагает построение многоуровневых моделей изменений, при этом первый уровень является уровнем множественных измерений, а второй — оценивания индивидуальных различий:

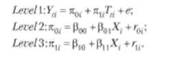
Для ЛИ модель на первом уровне описывает интраиндивидуальные изменения в показателях интересующей исследователя переменной в течение времени (каждый испытуемый может иметь свою индивидуальную траекторию изменения, что задается включением в уравнение термина случайной ошибки, ef¡), модель на втором уровне задаст межиндивидуальные различия в темпах изменений. При этом начальный уровень (тт0|.) и динамические показатели роста (ßh) могут быть смоделированы в терминах предикторов (как дихотомических — принадлежность к группе, — так и количественных). Таким образом, путем концептуального переосмысления и математического переопределения единиц анализа лонгитюдных данных через сведение их в иерархическую систему ULM можно оценивать и моделировать как интраиндивидуальные различия, так и межиндивидуальные различия в кривых развития, использовать пропущенные значения (в рамках метода полного максимального подобия) и проверять сложные гипотезы о нелинейных изменениях.

SEM как подход к моделированию лонгитюдных данных предполагает построение структурных моделей латентных изменений. Достоинствами этого метода является его соответствие интуитивным графическим способам (диаграммам) отображения структурных моделей, возможность операционализации ошибки измерения через построение моделей измерения. Итак, 5£М-подход позволяет проверять гипотезы об изменениях в латентных переменных [Bollen, Curran, 2006]. Тем не менее этот метод с большим трудом позволяет использовать пропущенные данные и моделировать нелинейные изменения.

Использование HLM- или 5£М-подхода в большинстве случаев является вопросом предпочтения конкретного исследователя, и чаще всего результаты использования обоих подходов являются идентичными. Оба метода на сегодняшний день являются де-факто стандартом в лонгитюдных исследованиях за рубежом, но лишь недавно стали использоваться в отечественных публикациях. Пока в отечественной психологии опубликованы только единичные примеры иерархического линейного моделирования [Корнилов и др., 2009; Корнилова и др., 2010].

Экскурс 19.2

Рассмотрим пример из названных исследований, в котором лонгитюдно отслеживалась успеваемость нескольких когорт студентов на протяжении всего времени их обучения в вузе и на материале выборки в более чем 450 человек [Корнилов и др., 2009]. При построении двухуровневой модели в нем установлена нелинейная динамика успеваемости студентов в высшей школе, а именно: снижение успеваемости на втором курсе.

Рис. 19.4. График средних сырых значений успешности обучения студентов за 9 сессий

Первичный анализ графика средней траектории изменения успешности обучения (рис. 19.4) показал, что применение единой линейной модели для всего времени обучения невозможно, поэтому в дальнейшем применялся метод кусочного иерархического линейного моделирования, предполагающего задание отдельных темпов роста для четырех различных временных периодов1: с 1-й по 3-ю сессию, с 3-й по 5-ю, с 5-й по 8-ю и с 8-й по 9-ю сессию.

Важным результатом стало выявление на втором уровне модели психологических предикторов исходной успеваемости, темпов ее снижения и возрастания. Так, начальный статус предсказывался уровнем развития аналитических способностей студентов, а креативность и практический интеллект выступили факторами, "защищающими" от снижения успеваемости. Использование #£М-методологии при обработке данных позволило провести оценку предикторов динамических характеристик успешности обучения, выйдя за пределы традиционных для отечественной психологии образования моделей исследований.

Итак, сложности применения лонгитюдного метода в психологии связаны со спецификой проверяемых в ЛИ гипотез о развитии, несмотря на синонимичное звучание (гипотезы о развитии) выходящих за пределы одной только психологии развития и проверяемых в самых различных областях психологии (от когнитивной до клинической). Анализ временной динамики показателей изучаемого процесса в современных исследованиях осуществляется не только в классических схемах лонгитюда, но и дополняет самые различные схемы — от контроля влияния фактора времени до моделирования осуществляемых или наблюдаемых влияний НП на показатели ЗП (с контролем смешивающихся переменных в квазиэкспериментальных и собственно экспериментальных исследованиях). При этом к обычным процедурам оценки валидности исследования добавляется ряд специфичных для лонигитюда критериев оценки качества исследования.

Современные способы статистической обработки лонгитюдных данных позволяют выявлять скрытые тенденции, неочевидные кривые развития, которые не всегда можно репрезентировать диаграммами и обычными функциональными графиками. Лонгитюдный метод в современном его звучании предполагает такую спецификацию психологом целей своего исследования, при которой ему совершенно необходимо владеть современными способами многомерной статистики и современными программами, позволяющими моделировать изучаемые зависимости.